It is designed to work with patterned data. Famous examples of problems related to patterned data are:
It allows for single or joint modeling of, for instance, genes and proteins.
Patterns package and dedicated to get specific features for the inferred network such as sparsity, robust links, high confidence links or stable through resampling links.
lars packageglmnet package. An unweighted and a weighted version of the algorithm are availablespls packageelasticnet packagec060 package implementation of stability selectionc060 package implementation of stability selection that I created for the packagelars package with light random Gaussian noise added to the explanatory variablesselectboost package. The selectboost algorithm looks for the more stable links against resampling that takes into account the correlated structure of the predictorsselectboost.The weights are viewed as a penalty factors in the penalized regression model: it is a number that multiplies the lambda value in the minimization problem to allow differential shrinkage, Friedman et al. 2010, equation 1 page 3. If equal to 0, it implies no shrinkage, and that variable is always included in the model. Default is 1 for all variables. Infinity means that the variable is excluded from the model. Note that the weights are rescaled to sum to the number of variables.
A word for those that have been using our seminal work, the Cascade package that we created several years ago and that was a very efficient network reverse engineering tool for cascade networks (Jung, N., Bertrand, F., Bahram, S., Vallat, L., and Maumy-Bertrand, M. (2014), https://doi.org/10.1093/bioinformatics/btt705, https://cran.r-project.org/package=Cascade, https://github.com/fbertran/Cascade and https://fbertran.github.io/Cascade/).
The Patterns package is more than (at least) a threeway major extension of the Cascade package :
Cascade package only 1 group for each timepoint could be created, which prevented the users to create homogeneous clusters of genes in datasets that featured more than a few dozens of genes.Cascade package only 1 shape was provided:
Cascade.Hence the Patterns package should be viewed more as a completely new modelling tools than as an extension of the Cascade package.
This website and these examples were created by F. Bertrand and M. Maumy-Bertrand.
You can install the released version of Patterns from CRAN with:
You can install the development version of Patterns from github with:
Import Cascade Data (repeated measurements on several subjects) from the CascadeData package and turn them into a micro array object. The second line makes sure the CascadeData package is installed.
if(!require(CascadeData)){install.packages("CascadeData")}
data(micro_US)
micro_US<-as.micro_array(micro_US[1:100,],time=c(60,90,210,390),subject=6)
str(micro_US)
#> Formal class 'micro_array' [package "Patterns"] with 7 slots
#> ..@ microarray: num [1:100, 1:24] 103.2 26 70.7 213.7 13.7 ...
#> .. ..- attr(*, "dimnames")=List of 2
#> .. .. ..$ : chr [1:100] "1007_s_at" "1053_at" "117_at" "121_at" ...
#> .. .. ..$ : chr [1:24] "N1_US_T60" "N1_US_T90" "N1_US_T210" "N1_US_T390" ...
#> ..@ name : chr [1:100] "1007_s_at" "1053_at" "117_at" "121_at" ...
#> ..@ gene_ID : num 0
#> ..@ group : num 0
#> ..@ start_time: num 0
#> ..@ time : num [1:4] 60 90 210 390
#> ..@ subject : num 6Get a summay and plots of the data:
summary(micro_US)
#> N1_US_T60 N1_US_T90 N1_US_T210
#> Min. : 12.2 Min. : 12.9 Min. : 1.5
#> 1st Qu.: 177.7 1st Qu.: 198.7 1st Qu.: 189.0
#> Median : 513.0 Median : 499.4 Median : 608.5
#> Mean :1386.6 Mean :1357.7 Mean :1450.4
#> 3rd Qu.:1912.3 3rd Qu.:1883.4 3rd Qu.:2050.2
#> Max. :6348.4 Max. :6507.3 Max. :6438.5
#> N1_US_T390 N2_US_T60 N2_US_T90
#> Min. : 10.1 Min. : 16.7 Min. : 3.4
#> 1st Qu.: 196.7 1st Qu.: 212.4 1st Qu.: 185.7
#> Median : 541.2 Median : 584.1 Median : 501.5
#> Mean :1331.2 Mean :1381.9 Mean :1345.4
#> 3rd Qu.:1646.2 3rd Qu.:1616.2 3rd Qu.:1830.5
#> Max. :6351.4 Max. :6149.3 Max. :6090.8
#> N2_US_T210 N2_US_T390 N3_US_T60
#> Min. : 5.5 Min. : 6.1 Min. : 1.9
#> 1st Qu.: 214.7 1st Qu.: 230.1 1st Qu.: 187.4
#> Median : 596.0 Median : 601.8 Median : 611.4
#> Mean :1410.5 Mean :1403.7 Mean :1365.4
#> 3rd Qu.:2005.8 3rd Qu.:1901.7 3rd Qu.:1855.2
#> Max. :6160.6 Max. :6143.1 Max. :6636.6
#> N3_US_T90 N3_US_T210 N3_US_T390
#> Min. : 10.3 Min. : 3.3 Min. : 6.6
#> 1st Qu.: 194.6 1st Qu.: 177.8 1st Qu.: 222.6
#> Median : 576.2 Median : 552.2 Median : 593.7
#> Mean :1381.2 Mean :1310.1 Mean :1427.1
#> 3rd Qu.:2040.2 3rd Qu.:1784.5 3rd Qu.:2131.7
#> Max. :6515.5 Max. :6530.4 Max. :6177.2
#> N4_US_T60 N4_US_T90 N4_US_T210
#> Min. : 20.2 Min. : 15.6 Min. : 19.8
#> 1st Qu.: 199.3 1st Qu.: 215.4 1st Qu.: 207.0
#> Median : 610.8 Median : 614.0 Median : 544.9
#> Mean :1505.1 Mean :1526.7 Mean :1401.6
#> 3rd Qu.:2198.1 3rd Qu.:2168.9 3rd Qu.:1831.2
#> Max. :6986.2 Max. :7148.0 Max. :6820.0
#> N4_US_T390 N5_US_T60 N5_US_T90
#> Min. : 9.3 Min. : 3.4 Min. : 10.0
#> 1st Qu.: 197.8 1st Qu.: 213.2 1st Qu.: 209.8
#> Median : 590.7 Median : 609.4 Median : 561.3
#> Mean :1458.8 Mean :1498.2 Mean :1424.8
#> 3rd Qu.:1984.8 3rd Qu.:2008.7 3rd Qu.:1906.5
#> Max. :6762.3 Max. :7268.2 Max. :6857.8
#> N5_US_T210 N5_US_T390 N6_US_T60
#> Min. : 10.7 Min. : 16.5 Min. : 13.0
#> 1st Qu.: 202.0 1st Qu.: 208.2 1st Qu.: 207.5
#> Median : 555.6 Median : 570.5 Median : 516.2
#> Mean :1394.1 Mean :1435.3 Mean :1412.9
#> 3rd Qu.:1923.9 3rd Qu.:1867.8 3rd Qu.:2037.4
#> Max. :6574.0 Max. :6896.6 Max. :6898.1
#> N6_US_T90 N6_US_T210 N6_US_T390
#> Min. : 6.6 Min. : 3.8 Min. : 14.4
#> 1st Qu.: 198.6 1st Qu.: 203.9 1st Qu.: 195.8
#> Median : 530.6 Median : 578.0 Median : 580.0
#> Mean :1388.3 Mean :1416.5 Mean :1360.8
#> 3rd Qu.:1889.8 3rd Qu.:2030.8 3rd Qu.:1872.6
#> Max. :6749.4 Max. :6490.0 Max. :6780.2



There are several functions to carry out gene selection before the inference. They are detailed in the vignette of the package.
Let’s simulate some cascade data and then do some reverse engineering.
We first design the F matrix for \(T_i=4\) times and \(Ngrp=4\) groups. The Fmatobject is an array of sizes \((T_i,T-i,Ngrp^2)=(4,4,16)\).
Ti<-4
Ngrp<-4
Fmat=array(0,dim=c(Ti,Ti,Ngrp^2))
for(i in 1:(Ti^2)){
if(((i-1) %% Ti) > (i-1) %/% Ti){
Fmat[,,i][outer(1:Ti,1:Ti,function(x,y){0<(x-y) & (x-y)<2})]<-1
}
}The Patterns function CascadeFinit is an utility function to easily define such an F matrix.
Fbis=Patterns::CascadeFinit(Ti,Ngrp,low.trig=FALSE)
str(Fbis)
#> num [1:4, 1:4, 1:16] 0 0 0 0 0 0 0 0 0 0 ...Check if the two matrices Fmat and Fbis are identical.
End of F matrix definition.
Fmat[,,3]<-Fmat[,,3]*0.2
Fmat[3,1,3]<-1
Fmat[4,2,3]<-1
Fmat[,,4]<-Fmat[,,3]*0.3
Fmat[4,1,4]<-1
Fmat[,,8]<-Fmat[,,3]We set the seed to make the results reproducible and draw a scale free random network.
set.seed(1)
Net<-Patterns::network_random(
nb=100,
time_label=rep(1:4,each=25),
exp=1,
init=1,
regul=round(rexp(100,1))+1,
min_expr=0.1,
max_expr=2,
casc.level=0.4
)
Net@F<-Fmat
str(Net)
#> Formal class 'network' [package "Patterns"] with 6 slots
#> ..@ network: num [1:100, 1:100] 0 0 0 0 0 0 0 0 0 0 ...
#> ..@ name : chr [1:100] "gene 1" "gene 2" "gene 3" "gene 4" ...
#> ..@ F : num [1:4, 1:4, 1:16] 0 0 0 0 0 0 0 0 0 0 ...
#> ..@ convF : num [1, 1] 0
#> ..@ convO : num 0
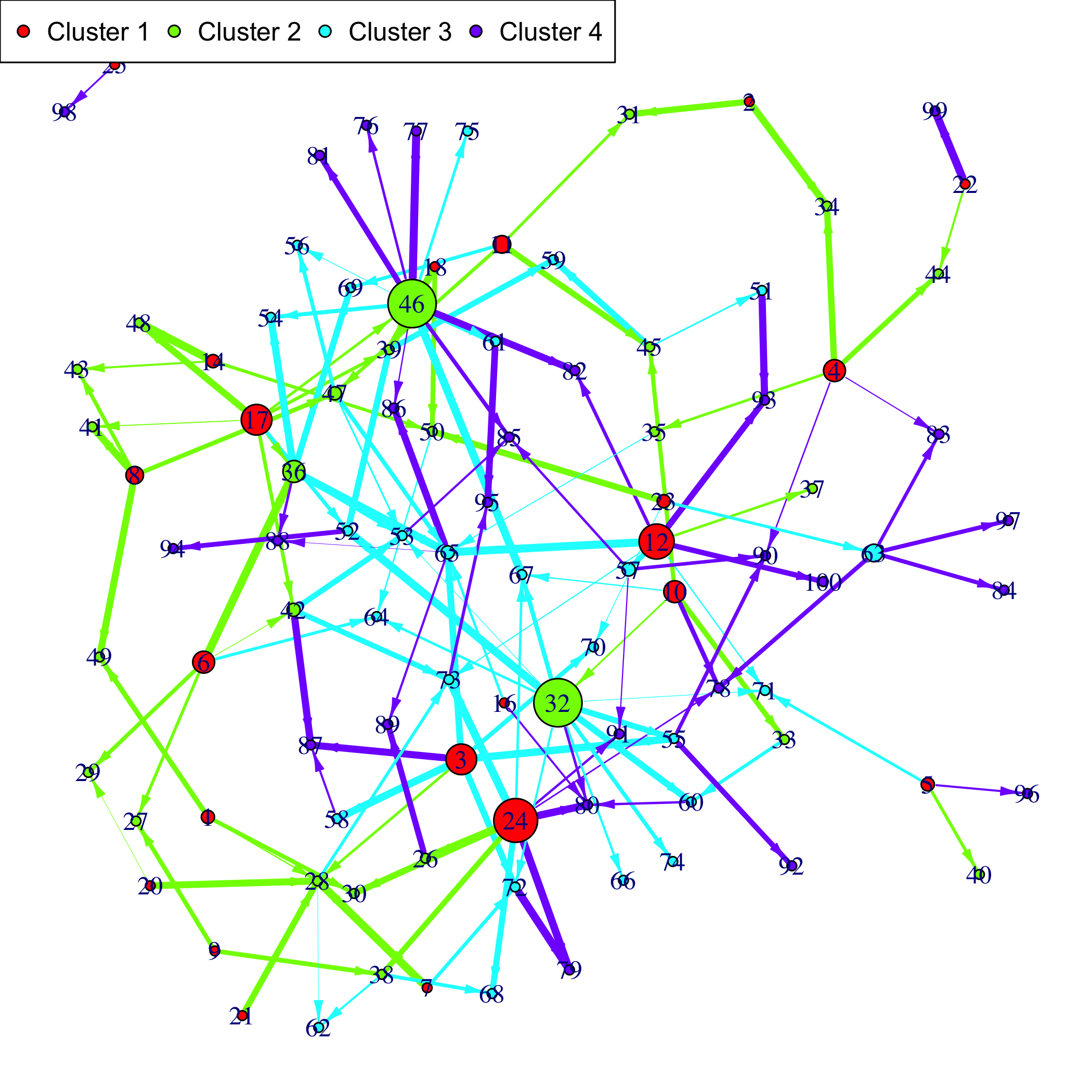
#> ..@ time_pt: int [1:4] 1 2 3 4Plot the simulated network.

If a gene clustering is known, it can be used as a coloring scheme.

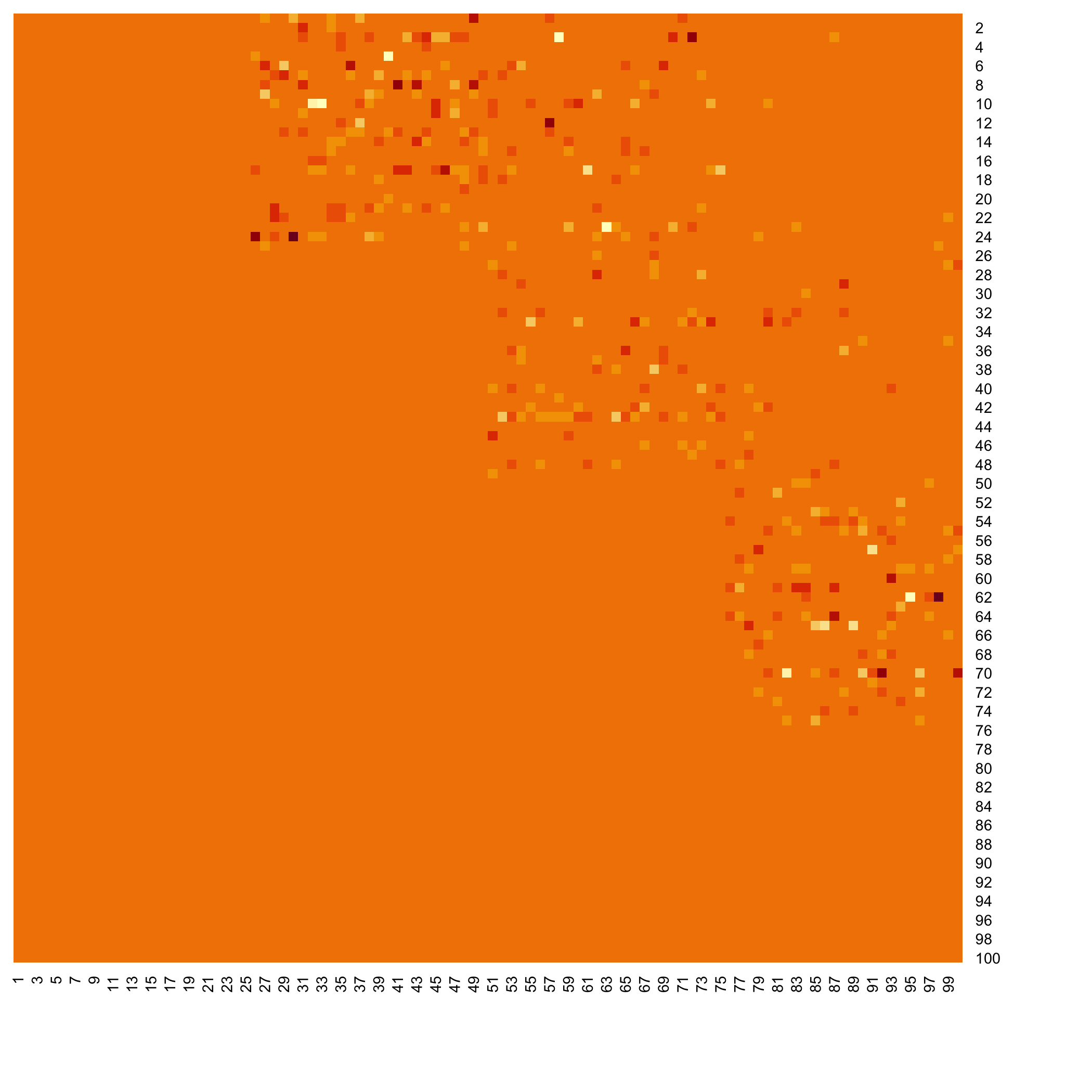
Plot the F matrix, for low dimensional F matrices.

Plot the F matrix using the pixmap package, for high dimensional F matrices.

We simulate gene expression according to the network that was previously drawn
set.seed(1)
M <- Patterns::gene_expr_simulation(
network=Net,
time_label=rep(1:4,each=25),
subject=5,
peak_level=200,
act_time_group=1:4)
str(M)
#> Formal class 'micro_array' [package "Patterns"] with 7 slots
#> ..@ microarray: num [1:100, 1:20] 86.1 -146.8 228.3 505.1 -36.6 ...
#> .. ..- attr(*, "dimnames")=List of 2
#> .. .. ..$ : chr [1:100] "gene 1" "gene 2" "gene 3" "gene 4" ...
#> .. .. ..$ : chr [1:20] "log(S/US) : P1T1" "log(S/US) : P1T2" "log(S/US) : P1T3" "log(S/US) : P1T4" ...
#> ..@ name : chr [1:100] "gene 1" "gene 2" "gene 3" "gene 4" ...
#> ..@ gene_ID : num 0
#> ..@ group : int [1:100] 1 1 1 1 1 1 1 1 1 1 ...
#> ..@ start_time: num 0
#> ..@ time : int [1:4] 1 2 3 4
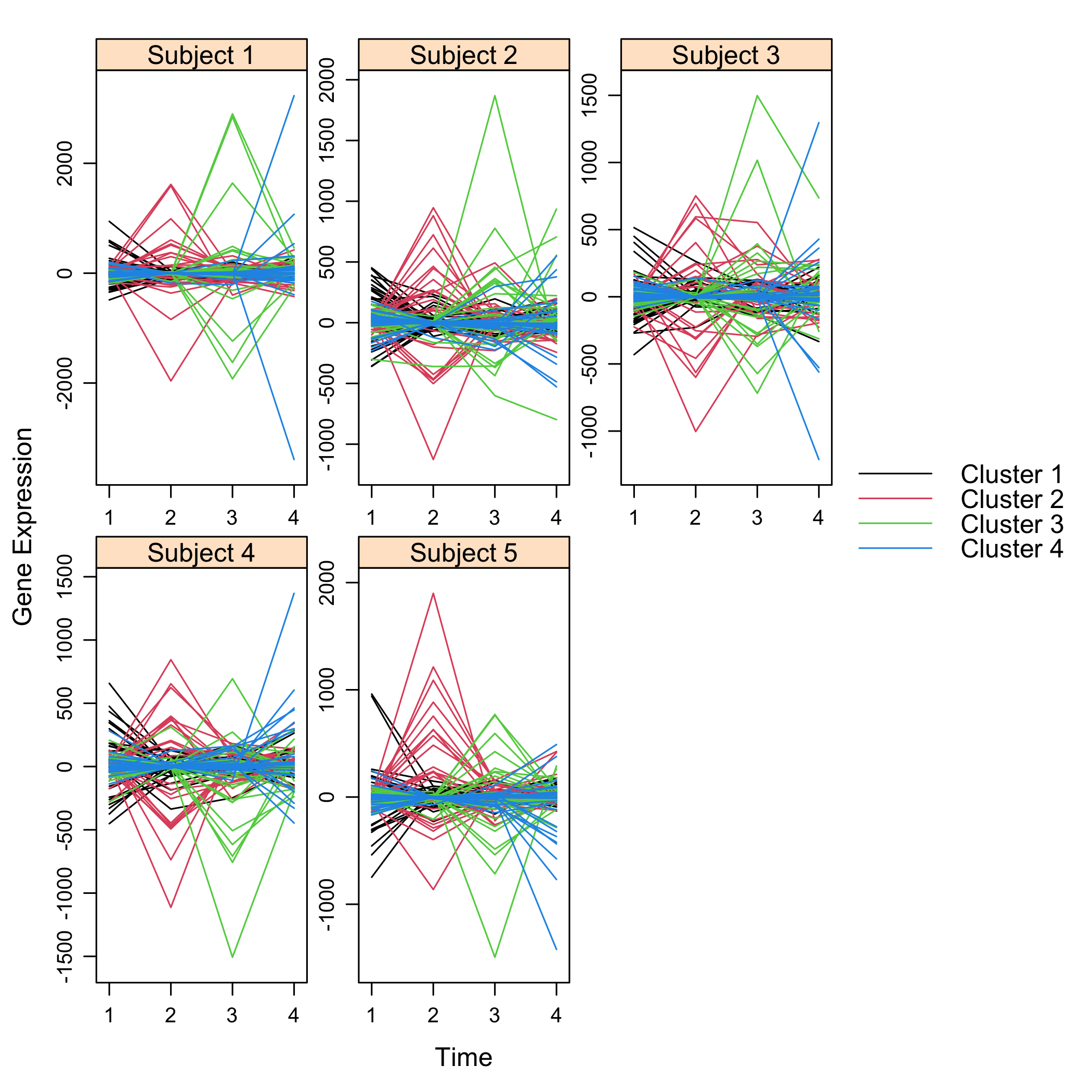
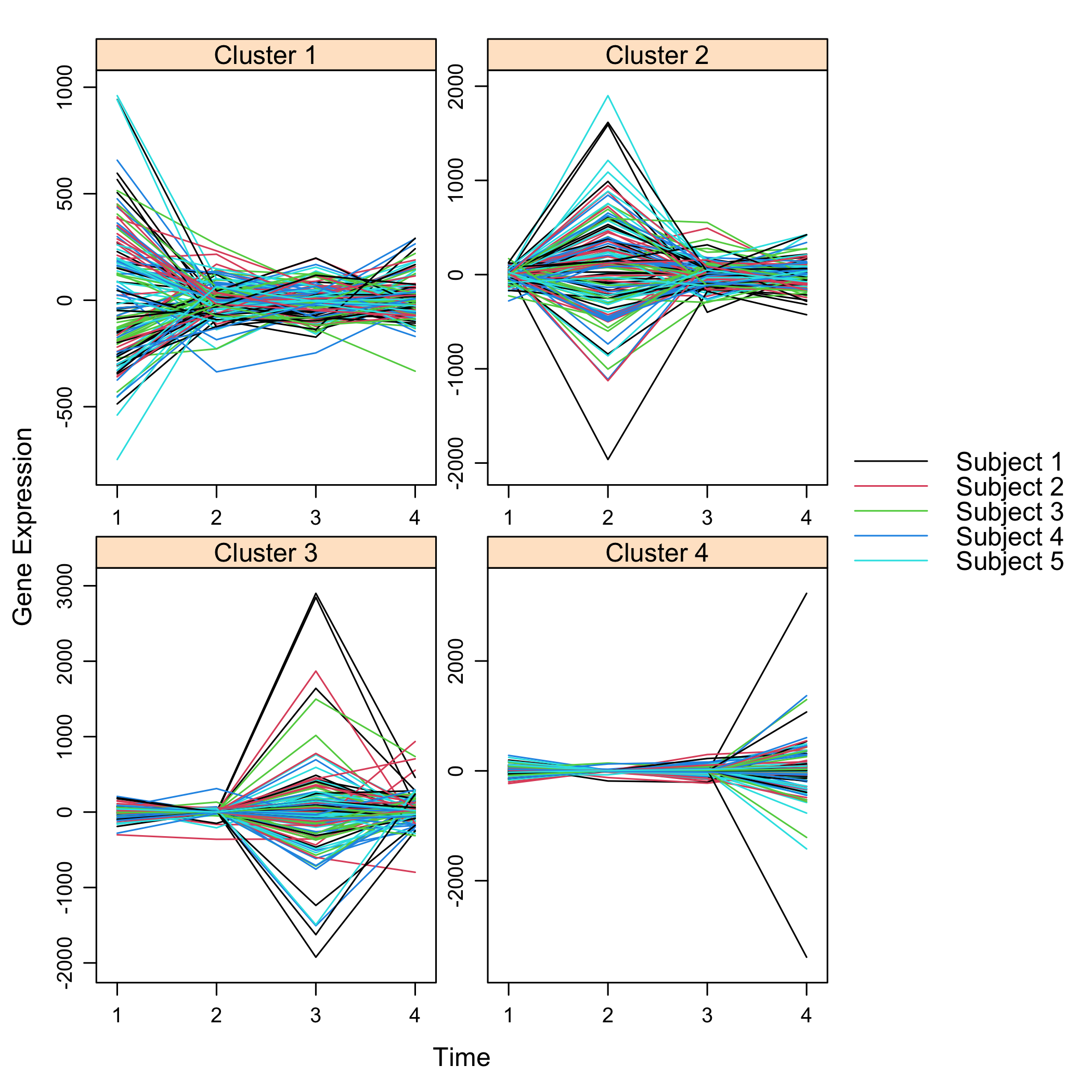
#> ..@ subject : num 5Get a summay and plots of the simulated data:
summary(M)
#> log(S/US) : P1T1 log(S/US) : P1T2 log(S/US) : P1T3
#> Min. :-486.823 Min. :-1962.641 Min. :-1923.74
#> 1st Qu.: -54.618 1st Qu.: -23.300 1st Qu.: -71.99
#> Median : -8.319 Median : 0.000 Median : -3.85
#> Mean : 8.799 Mean : 22.064 Mean : 20.72
#> 3rd Qu.: 69.340 3rd Qu.: 9.707 3rd Qu.: 33.00
#> Max. : 942.229 Max. : 1616.469 Max. : 2899.61
#> log(S/US) : P1T4 log(S/US) : P2T1 log(S/US) : P2T2
#> Min. :-3391.76 Min. :-359.82 Min. :-1126.13
#> 1st Qu.: -58.69 1st Qu.: -39.27 1st Qu.: -14.15
#> Median : 1.53 Median : 12.54 Median : 0.00
#> Mean : 19.82 Mean : 21.35 Mean : 20.02
#> 3rd Qu.: 69.45 3rd Qu.: 73.02 3rd Qu.: 28.54
#> Max. : 3231.17 Max. : 451.61 Max. : 946.22
#> log(S/US) : P2T3 log(S/US) : P2T4 log(S/US) : P3T1
#> Min. :-600.757 Min. :-797.980 Min. :-430.696
#> 1st Qu.: -49.998 1st Qu.: -73.700 1st Qu.: -65.939
#> Median : -7.749 Median : -9.760 Median : 1.392
#> Mean : 23.579 Mean : 8.361 Mean : 4.032
#> 3rd Qu.: 67.216 3rd Qu.: 62.297 3rd Qu.: 62.391
#> Max. :1869.077 Max. : 935.321 Max. : 514.510
#> log(S/US) : P3T2 log(S/US) : P3T3 log(S/US) : P3T4
#> Min. :-1003.575 Min. :-718.3926 Min. :-1211.592
#> 1st Qu.: -3.637 1st Qu.: -43.3783 1st Qu.: -61.300
#> Median : 0.000 Median : -0.3233 Median : -4.124
#> Mean : 11.431 Mean : 19.7553 Mean : 5.993
#> 3rd Qu.: 36.945 3rd Qu.: 69.6650 3rd Qu.: 62.634
#> Max. : 752.066 Max. :1497.5790 Max. : 1296.563
#> log(S/US) : P4T1 log(S/US) : P4T2 log(S/US) : P4T3
#> Min. :-451.370 Min. :-1113.1785 Min. :-1506.536
#> 1st Qu.: -44.107 1st Qu.: -8.8769 1st Qu.: -48.512
#> Median : 7.193 Median : 0.0000 Median : 4.243
#> Mean : 16.034 Mean : 0.9469 Mean : -28.544
#> 3rd Qu.: 62.840 3rd Qu.: 33.2306 3rd Qu.: 46.374
#> Max. : 657.434 Max. : 844.0070 Max. : 694.220
#> log(S/US) : P4T4 log(S/US) : P5T1 log(S/US) : P5T2
#> Min. :-446.40 Min. :-747.865 Min. :-862.59
#> 1st Qu.: -56.95 1st Qu.: -78.166 1st Qu.: -15.10
#> Median : 3.71 Median : -8.900 Median : 0.00
#> Mean : 28.74 Mean : -7.693 Mean : 66.20
#> 3rd Qu.: 64.89 3rd Qu.: 45.926 3rd Qu.: 31.74
#> Max. :1368.62 Max. : 960.419 Max. :1899.57
#> log(S/US) : P5T3 log(S/US) : P5T4
#> Min. :-1493.607 Min. :-1420.740
#> 1st Qu.: -59.853 1st Qu.: -32.799
#> Median : -2.776 Median : 4.008
#> Mean : -13.865 Mean : -12.332
#> 3rd Qu.: 40.324 3rd Qu.: 59.892
#> Max. : 770.655 Max. : 489.916









We infer the new network using subjectwise leave one out cross-validation (default setting): all measurements from the same subject are removed from the dataset). The inference is carried out with a general Fshape.
Net_inf_P <- Patterns::inference(M, cv.subjects=TRUE)
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.01
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00522
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0034
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00235
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00181
#> We are at step : 6
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00142
#> We are at step : 7
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00117
#> We are at step : 8
#> Computing Group (out of 4) :
#> 1.........................
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00098

Plot of the inferred F matrix

Heatmap of the inferred coefficients of the Omega matrix

Default values fot the \(F\) matrices. The Finit matrix (starting values for the algorithm). In our case, the Finitobject is an array of sizes \((T_i,T-i,Ngrp^2)=(4,4,16)\).
Ti<-4;
ngrp<-4
nF<-ngrp^2
Finit<-array(0,c(Ti,Ti,nF))
for(ii in 1:nF){
if((ii%%(ngrp+1))==1){
Finit[,,ii]<-0
} else {
Finit[,,ii]<-cbind(rbind(rep(0,Ti-1),diag(1,Ti-1)),rep(0,Ti))+rbind(cbind(rep(0,Ti-1),diag(1,Ti-1)),rep(0,Ti))
}
}The Fshape matrix (default shape for F matrix the algorithm). Any interaction between groups and times are permitted except the retro-actions (a group on itself, or an action at the same time for an actor on another one).
Fshape<-array("0",c(Ti,Ti,nF))
for(ii in 1:nF){
if((ii%%(ngrp+1))==1){
Fshape[,,ii]<-"0"
} else {
lchars <- paste("a",1:(2*Ti-1),sep="")
tempFshape<-matrix("0",Ti,Ti)
for(bb in (-Ti+1):(Ti-1)){
tempFshape<-replaceUp(tempFshape,matrix(lchars[bb+Ti],Ti,Ti),-bb)
}
tempFshape <- replaceBand(tempFshape,matrix("0",Ti,Ti),0)
Fshape[,,ii]<-tempFshape
}
}Any other form can be used. A “0” coefficient is missing from the model. It allows testing the best structure of an “F” matrix and even performing some significance tests of hypothses on the structure of the \(F\) matrix.
The IndicFshape function allows to design custom F matrix for cascade networks with equally spaced measurements by specifying the zero and non zero \(F_{ij}\) cells of the \(F\) matrix. It is useful for models featuring several clusters of actors that are activated at the time. Let’s define the following indicatrix matrix (action of all groups on each other, which is not a possible real modeling setting and is only used as an example):
TestIndic=matrix(!((1:(Ti^2))%%(ngrp+1)==1),byrow=TRUE,ngrp,ngrp)
TestIndic
#> [,1] [,2] [,3] [,4]
#> [1,] FALSE TRUE TRUE TRUE
#> [2,] TRUE FALSE TRUE TRUE
#> [3,] TRUE TRUE FALSE TRUE
#> [4,] TRUE TRUE TRUE FALSEFor that choice, we get those init and shape \(F\) matrices.
IndicFinit(Ti,ngrp,TestIndic)
#> , , 1
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 0 0 0 0
#> [3,] 0 0 0 0
#> [4,] 0 0 0 0
#>
#> , , 2
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 3
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 4
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 5
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 6
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 0 0 0 0
#> [3,] 0 0 0 0
#> [4,] 0 0 0 0
#>
#> , , 7
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 8
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 9
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 10
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 11
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 0 0 0 0
#> [3,] 0 0 0 0
#> [4,] 0 0 0 0
#>
#> , , 12
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 13
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 14
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 15
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 1 0 0 0
#> [3,] 1 1 0 0
#> [4,] 1 1 1 0
#>
#> , , 16
#>
#> [,1] [,2] [,3] [,4]
#> [1,] 0 0 0 0
#> [2,] 0 0 0 0
#> [3,] 0 0 0 0
#> [4,] 0 0 0 0
IndicFshape(Ti,ngrp,TestIndic)
#> , , 1
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "0" "0" "0" "0"
#> [3,] "0" "0" "0" "0"
#> [4,] "0" "0" "0" "0"
#>
#> , , 2
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 3
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 4
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 5
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 6
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "0" "0" "0" "0"
#> [3,] "0" "0" "0" "0"
#> [4,] "0" "0" "0" "0"
#>
#> , , 7
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 8
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 9
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 10
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 11
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "0" "0" "0" "0"
#> [3,] "0" "0" "0" "0"
#> [4,] "0" "0" "0" "0"
#>
#> , , 12
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 13
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 14
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 15
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "a1" "0" "0" "0"
#> [3,] "a2" "a1" "0" "0"
#> [4,] "a3" "a2" "a1" "0"
#>
#> , , 16
#>
#> [,1] [,2] [,3] [,4]
#> [1,] "0" "0" "0" "0"
#> [2,] "0" "0" "0" "0"
#> [3,] "0" "0" "0" "0"
#> [4,] "0" "0" "0" "0"Those \(F\) matrices are lower diagonal ones to enforce that an observed value at a given time can only be predicted by a value that was observed in the past only (i.e. neither at the same moment or in the future).
The plotF is convenient to display F matrices. Here are the the displays of the three \(F\) matrices we have just introduced.



We now fit the model with an \(F\) matrix that is designed for cascade networks.
Specific Fshape
Net_inf_P_S <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4))
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0074
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00314
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0019
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00131
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00101
#> We are at step : 6
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00081

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network. They reflect the use of a special \(F\) matrix. It is an example of an F matrix specifically designed to deal with cascade networks.

There are many fitting functions provided with the Patterns package in order to search for specific features for the inferred network such as sparsity, robust links, high confidence links or stable through resampling links. :
lars packageglmnet package. An unweighted and a weighted version of the algorithm are availablespls packageelasticnet packagec060 package implementation of stability selectionc060 package implementation of stability selectionlars package with light random Gaussian noise added to the explanatory variablesselectboost package implementation of the selectboost algorithm to look for the more stable links against resampling that takes into account the correlated structure of the predictors. If no weights are provided, equal weigths are for all the variables (=non weighted case).Net_inf_P_Lasso2 <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="LASSO2")
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0069
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00229
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00153
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00114
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00086

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

We create a weighting vector to perform weighted lasso inference.
Net_inf_P_Lasso2_Weighted <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="LASSO2", priors=Weights_Net)
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0075
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 4e-04

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_SPLS <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="SPLS")
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0075
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00229
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00164
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00123
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00104
#> We are at step : 6
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00088

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_ELASTICNET <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="ELASTICNET")
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0074
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00402
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00289
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00223
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00178
#> We are at step : 6
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00142
#> We are at step : 7
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00121
#> We are at step : 8
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00107
#> We are at step : 9
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00095

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_stability <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="stability.c060")
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1mc.cores=2
#> 2mc.cores=2.........................
#> 3mc.cores=2.........................
#> 4mc.cores=2.........................
#> The convergence of the network is (L1 norm) : 0.0042
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1mc.cores=2
#> 2mc.cores=2.........................
#> 3mc.cores=2.........................
#> 4mc.cores=2.........................
#> The convergence of the network is (L1 norm) : 0.00095

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_StabWeight <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="stability.c060.weighted", priors=Weights_Net)
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1mc.cores=2
#> 2mc.cores=2 .........................
#> 3mc.cores=2 .........................
#> 4mc.cores=2 .........................
#> The convergence of the network is (L1 norm) : 0.0075
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1mc.cores=2
#> 2mc.cores=2 .........................
#> 3mc.cores=2 .........................
#> 4mc.cores=2 .........................
#> The convergence of the network is (L1 norm) : 0.00034

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_Robust <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="robust")
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0069
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00366
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00203
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00142
#> We are at step : 5
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00117
#> We are at step : 6
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00086

Plot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Weights_Net_1 <- Weights_Net
Weights_Net_1[,] <- 1
Net_inf_P_SelectBoost <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="selectboost.weighted",priors=Weights_Net_1)
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> Loading required namespace: SelectBoost
#>
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.0057
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00174
#> We are at step : 3
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00125
#> We are at step : 4
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00094

#>
#> Attaching package: 'Patterns'
#> The following object is masked from 'package:igraph':
#>
#> comparePlot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network

Net_inf_P_SelectBoostWeighted <- Patterns::inference(M, Finit=CascadeFinit(4,4), Fshape=CascadeFshape(4,4), fitfun="selectboost.weighted",priors=Weights_Net)
#> We are at step : 1
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.007
#> We are at step : 2
#> Computing Group (out of 4) :
#> 1
#> 2.........................
#> 3.........................
#> 4.........................
#> The convergence of the network is (L1 norm) : 0.00047

#>
#> Attaching package: 'Patterns'
#> The following object is masked from 'package:igraph':
#>
#> comparePlot of the inferred F matrix

Heatmap of the coefficients of the Omega matrix of the network
stats::heatmap(Net_inf_P_SelectBoostWeighted@network, Rowv = NA, Colv = NA, scale="none", revC=TRUE)
Such an analysis is only required if the model was not fitted using the stability selection or the selectboost algorithm.
Create an animation of the network with increasing cutoffs with an animated .gif format or a html webpage in the working directory.
data(network)
sequence<-seq(0,0.2,length.out=20)
evolution(network,sequence,type.ani = "gif", outdir=getwd())
evolution(network,sequence,type.ani = "html", outdir=getwd())#> Error in setwd(outdir): impossible de changer de répertoire de travail
#> Error in setwd(outdir): impossible de changer de répertoire de travail
Evolution of some properties of a reverse-engineered network with increasing cut-off values. 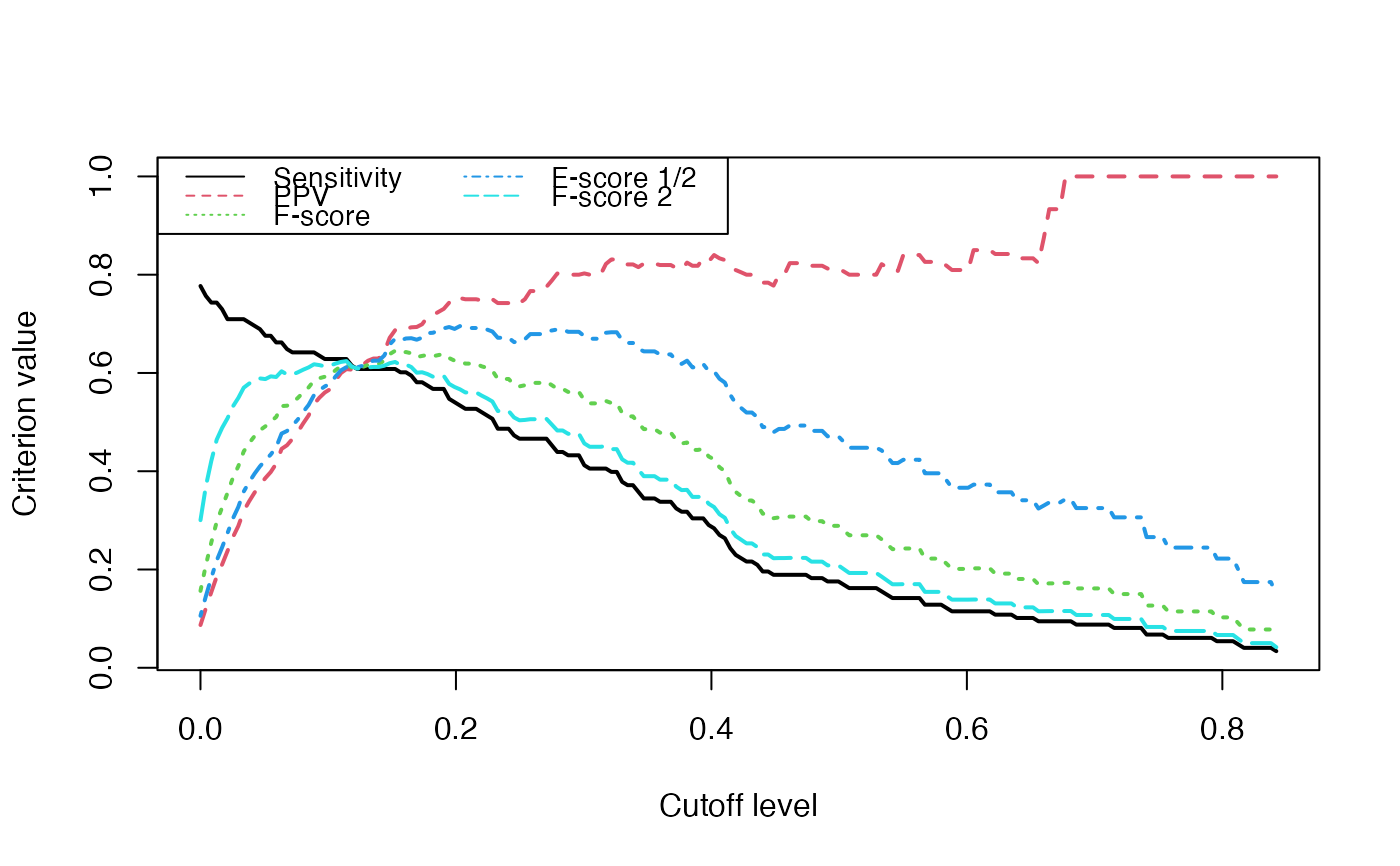
We switch to data that were derived from the inferrence of a real biological network and try to detect the optimal cutoff value: the best cutoff value for a network to fit a scale free network. The cutoff was validated only single group cascade networks (number of actors groups = number of timepoints) and for genes dataset. Instead of the cutoff function, manual curation or the stability selection or the selectboost algorithm should be used.
data("networkCascade")
set.seed(1)
cutoff(networkCascade)
#> [1] "This computation may be long"
#> [1] "1/10"
#> [1] "2/10"
#> [1] "3/10"
#> [1] "4/10"
#> [1] "5/10"
#> [1] "6/10"
#> [1] "7/10"
#> [1] "8/10"
#> [1] "9/10"
#> [1] "10/10"
#> [1] 0.000 0.007 0.423 0.388 0.236 0.631 0.952 0.976 0.825 0.362
#> $p.value
#> [1] 0.000 0.007 0.423 0.388 0.236 0.631 0.952 0.976 0.825 0.362
#>
#> $p.value.inter
#> [1] -0.04643835 0.14848083 0.28125541 0.36247646 0.33538710
#> [6] 0.60021707 0.92531630 0.98522398 0.79881816 0.37310221
#>
#> $sequence
#> [1] 0.00000000 0.04444444 0.08888889 0.13333333 0.17777778
#> [6] 0.22222222 0.26666667 0.31111111 0.35555556 0.40000000Analyze the network with a cutoff set to the previouly found 0.133 optimal value.
analyze_network(networkCascade,nv=0.133)
#> node betweenness degree output closeness
#> 1 1 0 3 0.6442821 2.5337730
#> 2 2 8 4 1.3784717 5.4211261
#> 3 3 0 6 1.3308218 6.1428682
#> 4 4 0 9 1.7531528 19.4060065
#> 5 5 0 2 0.6400128 2.5169831
#> 6 6 0 1 0.2725100 3.4520368
#> 7 7 0 0 0.0000000 0.0000000
#> 8 8 0 1 0.1483077 10.4595738
#> 9 9 4 4 0.7969945 3.4810740
#> 10 10 20 7 1.3485173 6.0949803
#> 11 11 0 4 0.8054122 16.2236448
#> 12 12 0 11 2.4624877 10.7417814
#> 13 13 0 0 0.0000000 0.0000000
#> 14 14 0 1 0.1882265 3.8504312
#> 15 15 0 5 1.5808956 13.7135886
#> 16 16 81 24 6.7716649 29.1131750
#> 17 17 0 9 2.0059124 11.2249512
#> 18 18 0 9 1.6083138 6.6506106
#> 19 19 0 0 0.0000000 0.0000000
#> 20 20 0 0 0.0000000 0.0000000
#> 21 21 0 0 0.0000000 0.0000000
#> 22 22 0 0 0.0000000 0.0000000
#> 23 23 0 0 0.0000000 0.0000000
#> 24 24 0 1 0.1607163 0.6320503
#> 25 25 0 0 0.0000000 0.0000000
#> 26 26 0 0 0.0000000 0.0000000
#> 27 27 0 8 3.2710799 13.9045595
#> 28 28 0 2 0.3957891 2.1118782
#> 29 29 0 0 0.0000000 0.0000000
#> 30 30 0 1 0.2255093 0.8868623
#> 31 31 0 0 0.0000000 0.0000000
#> 32 32 0 0 0.0000000 0.0000000
#> 33 33 0 0 0.0000000 0.0000000
#> 34 34 0 0 0.0000000 0.0000000
#> 35 35 0 6 1.4397935 5.6622868
#> 36 36 0 0 0.0000000 0.0000000
#> 37 37 0 0 0.0000000 0.0000000
#> 38 38 0 0 0.0000000 0.0000000
#> 39 39 0 0 0.0000000 0.0000000
#> 40 40 0 0 0.0000000 0.0000000
#> 41 41 0 0 0.0000000 0.0000000
#> 42 42 2 1 0.5205955 2.0473501
#> 43 43 0 0 0.0000000 0.0000000
#> 44 44 0 0 0.0000000 0.0000000
#> 45 45 0 0 0.0000000 0.0000000
#> 46 46 0 0 0.0000000 0.0000000
#> 47 47 0 0 0.0000000 0.0000000
#> 48 48 0 1 0.5096457 2.0042877
#> 49 49 1 1 0.1814386 0.7135450
#> 50 50 0 0 0.0000000 0.0000000
#> 51 51 0 0 0.0000000 0.0000000
#> 52 52 0 0 0.0000000 0.0000000
#> 53 53 0 0 0.0000000 0.0000000
#> 54 54 0 0 0.0000000 0.0000000
#> 55 55 0 0 0.0000000 0.0000000
#> 56 56 0 0 0.0000000 0.0000000
#> 57 57 5 1 0.7142387 2.8088919
#> 58 58 0 0 0.0000000 0.0000000
#> 59 59 0 0 0.0000000 0.0000000
#> 60 60 0 0 0.0000000 0.0000000
#> 61 61 0 0 0.0000000 0.0000000
#> 62 62 0 0 0.0000000 0.0000000
#> 63 63 0 1 0.1668072 0.6560038
#> 64 64 0 0 0.0000000 0.0000000
#> 65 65 0 0 0.0000000 0.0000000
#> 66 66 0 0 0.0000000 0.0000000
#> 67 67 0 0 0.0000000 0.0000000
#> 68 68 0 0 0.0000000 0.0000000
#> 69 69 0 0 0.0000000 0.0000000
#> 70 70 0 0 0.0000000 0.0000000
#> 71 71 0 0 0.0000000 0.0000000
#> 72 72 0 0 0.0000000 0.0000000
#> 73 73 4 1 0.1937648 0.7620205
#> 74 74 0 0 0.0000000 0.0000000
#> 75 75 0 0 0.0000000 0.0000000
#> 76 76 0 0 0.0000000 0.0000000
#> 77 77 0 0 0.0000000 0.0000000
#> 78 78 0 0 0.0000000 0.0000000
#> 79 79 0 0 0.0000000 0.0000000
#> 80 80 0 0 0.0000000 0.0000000
#> 81 81 0 0 0.0000000 0.0000000
#> 82 82 4 2 0.4875471 1.9173803
#> 83 83 4 1 0.2849991 1.1208180
#> 84 84 5 1 0.4477398 1.7608296
#> 85 85 4 1 0.2126269 0.8361995
#> 86 86 0 0 0.0000000 0.0000000
#> 87 87 0 0 0.0000000 0.0000000
#> 88 88 0 0 0.0000000 0.0000000
#> 89 89 0 0 0.0000000 0.0000000
#> 90 90 5 1 0.1522237 0.5986513
#> 91 91 3 1 0.2857613 1.1238157
#> 92 92 0 0 0.0000000 0.0000000
#> 93 93 0 1 0.1784006 0.7015976
#> 94 94 0 0 0.0000000 0.0000000
#> 95 95 0 0 0.0000000 0.0000000
#> 96 96 0 0 0.0000000 0.0000000
#> 97 97 0 0 0.0000000 0.0000000
#> 98 98 0 0 0.0000000 0.0000000
#> 99 99 0 0 0.0000000 0.0000000
#> 100 100 0 0 0.0000000 0.0000000
#> 101 101 0 0 0.0000000 0.0000000
#> 102 102 0 0 0.0000000 0.0000000
Import data.
library(Patterns)
library(CascadeData)
data(micro_S)
micro_S<-as.micro_array(micro_S,time=c(60,90,210,390),subject=6,gene_ID=rownames(micro_S))
data(micro_US)
micro_US<-as.micro_array(micro_US,time=c(60,90,210,390),subject=6,gene_ID=rownames(micro_US))Select early genes (t1 or t2):
Selection1<-geneSelection(x=micro_S,y=micro_US,20,wanted.patterns=rbind(c(0,1,0,0),c(1,0,0,0),c(1,1,0,0)))Section genes with first significant differential expression at t1:
Section genes with first significant differential expression at t2:
Select later genes (t3 or t4)
Selection4<-geneSelection(x=micro_S,y=micro_US,50,
wanted.patterns=rbind(c(0,0,1,0),c(0,0,0,1),c(1,1,0,0)))Merge those selections:
Selection<-unionMicro(Selection1,Selection2)
Selection<-unionMicro(Selection,Selection3)
Selection<-unionMicro(Selection,Selection4)
head(Selection)
#> $microarray
#> US60 US90 US210
#> 210226_at 0.82417544 0.9166931 0.7310784
#> 233516_s_at -0.27395188 -2.3695246 0.6511830
#> 202081_at 0.60477249 0.6599672 -0.1884742
#> 236719_at -2.07284086 -0.3123747 0.1792494
#> 236019_at -0.08175065 -0.3699708 -0.4315901
#> 1563563_at -1.44513486 1.6869516 -0.4297297
#>
#> $name
#> [1] "210226_at" "233516_s_at" "202081_at" "236719_at"
#> [5] "236019_at" "1563563_at"
#>
#> $gene_ID
#> [1] "210226_at" "233516_s_at" "202081_at" "236719_at"
#> [5] "236019_at" "1563563_at"
#>
#> $group
#> [1] 1 2 1 1 1 1
#>
#> $start_time
#> [1] 1 2 1 1 1 1
#>
#> $time
#> [1] 60 90 210 390
#>
#> $subject
#> [1] 6Summarize the final selection:
summary(Selection)
#> US60 US90 US210
#> Min. :-2.76841 Min. :-2.369525 Min. :-1.6147
#> 1st Qu.:-0.18028 1st Qu.:-0.181425 1st Qu.: 0.1985
#> Median : 0.05675 Median :-0.001924 Median : 0.9886
#> Mean : 0.05764 Mean : 0.278275 Mean : 0.9611
#> 3rd Qu.: 0.22438 3rd Qu.: 0.664063 3rd Qu.: 1.6918
#> Max. : 2.86440 Max. : 4.284675 Max. : 3.6727
#> US390 US60 US90
#> Min. :-2.60480 Min. :-2.7932 Min. :-2.49245
#> 1st Qu.:-0.03884 1st Qu.:-0.5547 1st Qu.:-0.01944
#> Median : 0.31766 Median :-0.3089 Median : 0.14977
#> Mean : 0.26428 Mean :-0.2917 Mean : 0.33720
#> 3rd Qu.: 0.57117 3rd Qu.:-0.1725 3rd Qu.: 0.48744
#> Max. : 2.54704 Max. : 2.0267 Max. : 3.37588
#> US210 US390 US60
#> Min. :-1.21606 Min. :-1.74407 Min. :-2.94444
#> 1st Qu.: 0.07966 1st Qu.:-0.26548 1st Qu.:-0.23136
#> Median : 0.72019 Median : 0.03616 Median :-0.04761
#> Mean : 0.73063 Mean : 0.06753 Mean : 0.22115
#> 3rd Qu.: 1.26164 3rd Qu.: 0.32496 3rd Qu.: 0.33157
#> Max. : 3.87950 Max. : 2.83321 Max. : 3.31723
#> US90 US210 US390
#> Min. :-0.9721 Min. :-1.9349 Min. :-3.8418
#> 1st Qu.:-0.1027 1st Qu.: 0.3254 1st Qu.:-0.1592
#> Median : 0.2548 Median : 1.2512 Median : 0.1538
#> Mean : 0.6479 Mean : 1.0485 Mean : 0.1219
#> 3rd Qu.: 1.0737 3rd Qu.: 1.8513 3rd Qu.: 0.6268
#> Max. : 4.3604 Max. : 4.4860 Max. : 1.9886
#> US60 US90 US210
#> Min. :-2.85438 Min. :-0.90355 Min. :-0.83324
#> 1st Qu.:-0.06031 1st Qu.:-0.08464 1st Qu.: 0.07605
#> Median : 0.03601 Median : 0.17135 Median : 0.52176
#> Mean : 0.14593 Mean : 0.41929 Mean : 0.62446
#> 3rd Qu.: 0.24568 3rd Qu.: 0.75565 3rd Qu.: 1.07821
#> Max. : 1.82903 Max. : 3.60640 Max. : 2.27744
#> US390 US60 US90
#> Min. :-0.96834 Min. :-1.38002 Min. :-2.94444
#> 1st Qu.: 0.01569 1st Qu.:-0.19910 1st Qu.:-0.01758
#> Median : 0.17370 Median :-0.07962 Median : 0.16080
#> Mean : 0.23854 Mean : 0.12972 Mean : 0.37123
#> 3rd Qu.: 0.45189 3rd Qu.: 0.26113 3rd Qu.: 0.61933
#> Max. : 1.90880 Max. : 2.31074 Max. : 3.24454
#> US210 US390 US60
#> Min. :-1.0271 Min. :-1.3636 Min. :-1.79176
#> 1st Qu.: 0.1459 1st Qu.:-0.1386 1st Qu.:-0.09822
#> Median : 0.7430 Median : 0.1492 Median : 0.03378
#> Mean : 0.7972 Mean : 0.1271 Mean : 0.27978
#> 3rd Qu.: 1.3922 3rd Qu.: 0.4825 3rd Qu.: 0.33548
#> Max. : 3.6213 Max. : 1.5979 Max. : 3.16035
#> US90 US210 US390
#> Min. :-3.20791 Min. :-1.4716 Min. :-1.95883
#> 1st Qu.:-0.03963 1st Qu.: 0.1292 1st Qu.:-0.04786
#> Median : 0.28261 Median : 0.8392 Median : 0.22472
#> Mean : 0.52529 Mean : 0.7903 Mean : 0.21171
#> 3rd Qu.: 1.03256 3rd Qu.: 1.4416 3rd Qu.: 0.42511
#> Max. : 3.19975 Max. : 2.8027 Max. : 2.14903


Plot the final selection:








This process could be improved by retrieve a real gene_ID using the bitr function of the ClusterProfiler package or by performing independent filtering using jetset package to only keep at most only probeset (the best one, if there is one good enough) per gene_ID.