The SPQR R package implements the semi-parametric
quantile regression (SPQR) method in Xu and Reich (2021) [1]. It allows flexible modeling of the conditional
distribution function and quantile function. The package provides three
estimation procedures: maximum likelihood estimation (MLE) and maximum a
posteriori (MAP) which are point estimates but computationally lighter,
and Markov chain Monte Carlo (MCMC) which is fully Bayesian but
computationally heavier. The MLE and MAP estimates are obtained using
the Adam routine in torch, whereas the MCMC estimate is
obtained using Stan-like Hamiltonian Monte Carlo (HMC) and no-U-turn
sampler (NUTS).
You can install the development version of SPQR from GitHub with:
# install.packages("devtools")
devtools::install_github("stevengxu/SPQR")Estimate normal mixture distribution:
library(SPQR)
set.seed(919)
n <- 200
X <- rbinom(n, 1, 0.5)
Y <- rnorm(n, X, 0.8)
control <- list(iter = 300, warmup = 200, thin = 1)
fit <- SPQR(X = X, Y = Y, method = "MCMC", control = control, normalize = TRUE, verbose = FALSE)
## summarize output
print(fit, showModel = TRUE)
#>
#> SPQR fitted using MCMC approach with ARD prior<U+0001F680>
#>
#> Model specification:
#> Layers
#> Input Output Activation
#> 1 10 tanh
#> 10 10 softmax
#>
#> MCMC diagnostics:
#> Final acceptance ratio is 0.94 and target is 0.9
#>
#> Expected log pointwise predictive density (elpd) estimates:
#> elpd.LOO = 92.49707, elpd.WAIC = 92.43618
#>
#> Elapsed time: 0.25 minutes
## plot estimated PDF with 95% credible bands
plotEstimator(fit, type = "PDF", X = 0, ci.level = 0.95)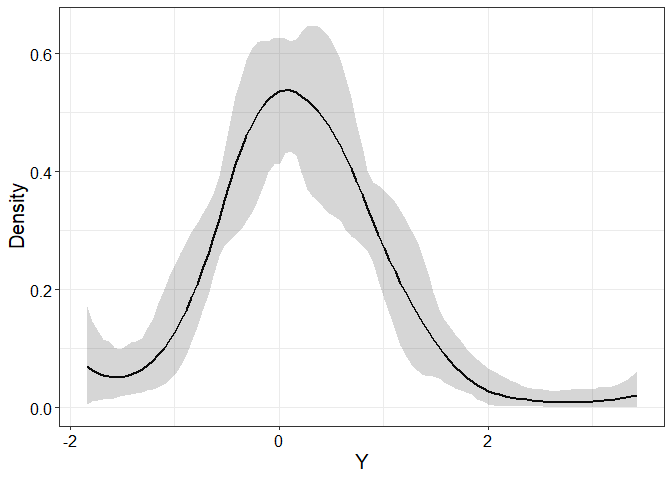
[1] Xu, S.G. and Reich, B.J., 2021. Bayesian nonparametric quantile process regression and estimation of marginal quantile effects. Biometrics.