

The package TRES implements the least squares and envelope estimation under the framework of tensor regression models. The general model-free envelope models can also be flexibly handled by the package via three types of envelope estimation algorithms: - Full Grassmannian (FG) algorithm. - 1D algorithm. - Envelope coordinate descent (ECD) algorithm - Partial least squares (PLS) type algorithm.
You can install the released version of TRES from CRAN with:
# Install the latest released version from CRAN
install.packages("TRES")
# Or the development version from GitHub:
remotes::install_github("leozeng15/TRES")This is a basic example providing you a guidance on how to use the primary function TRR.fit and several S3 methods in Tensor Response Regression (TRR) model. The ordinary least square method and 1D envelope method are implemented. See Li and Zhang (2017) for more background.
library(TRES)
## Load data "bat"
data("bat")
x <- bat$x
y <- bat$y
## Fitting with OLS and 1D envelope method.
fit_ols <- TRR.fit(x, y, method="standard")
fit_1D <- TRR.fit(x, y, u = c(14,14), method="1D") # pass envelope rank (14,14)
## Print cofficient
coef(fit_1D)
## Print the summary
summary(fit_1D)
## Extract the mean squared error, p-value and standard error from summary
summary(fit_1D)$mse
summary(fit_1D)$p_val
summary(fit_1D)$se
## Make the prediction on the original dataset
predict(fit_1D, x)
## Draw the plots of two-way coefficient tensor (i.e., matrix) and p-value tensor.
plot(fit_ols)
plot(fit_1D)The coefficients plots from OLS and 1D methods are aligned in the first row below, and the p-value plots from the two methods are aligned in the second row below.
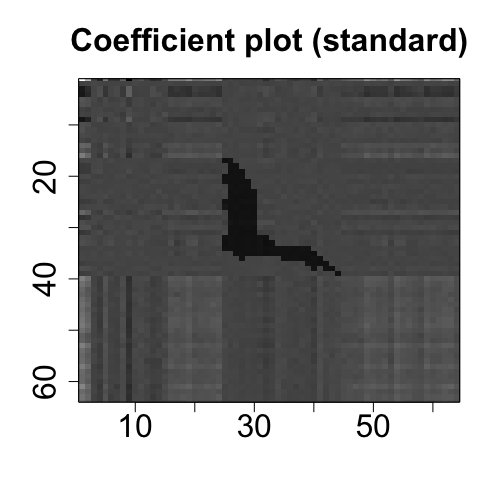
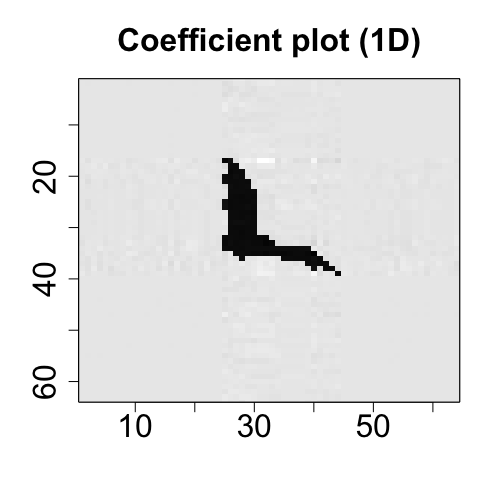
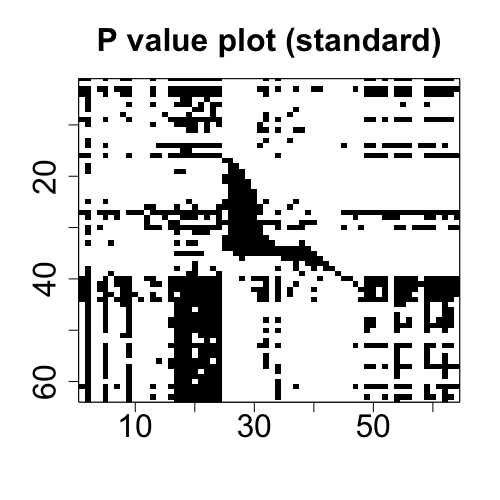
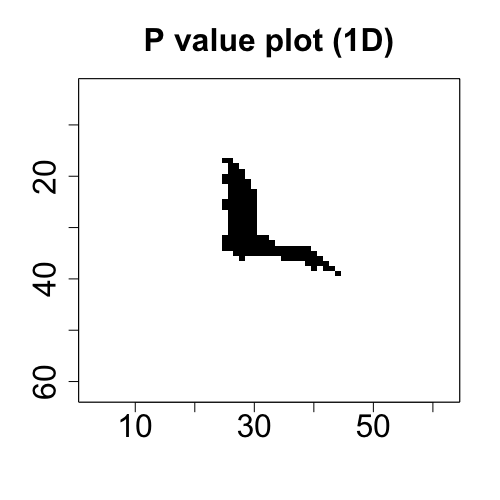
This example shows how to use the function MenU_sim to simulate the matrices M and U with envelope structure, and how to use different core functions to implement different envelope estimation algorithms. See Cook and Zhang (2016) for more details.
## Generate matrices M and U
p <- 50
u <- 5
n <- 200
data <- MenvU_sim(p, u, jitter = 1e-5, wishart = TRUE, n = n)
Gamma <- data$Gamma
M <- data$M
U <- data$U
## Use different envelope algorithms
G <- vector("list", 6)
G[[1]] <- simplsMU(M, U, u)
G[[2]] <- ECD(M, U, u)
G[[3]] <- manifold1D(M, U, u)
G[[4]] <- OptM1D(M, U, u)
G[[5]] <- manifoldFG(M, U, u)
G[[6]] <- OptMFG(M, U, u)1D algorithm: Cook, R.D. and Zhang, X., 2016. Algorithms for envelope estimation. Journal of Computational and Graphical Statistics, 25(1), pp.284-300.
TRR: Li, L. and Zhang, X., 2017. Parsimonious tensor response regression. Journal of the American Statistical Association, 112(519), pp.1131-1146.
TPR: Zhang, X. and Li, L., 2017. Tensor envelope partial least-squares regression. Technometrics, 59(4), pp.426-436.
ECD algorithm: Cook, R.D. and Zhang, X., 2018. Fast envelope algorithms. Statistica Sinica, 28(3), pp.1179-1197.
Zeng J., Wang W., Zhang X. (2021) TRES: An R Package for Tensor Regression and Envelope Algorithms. Journal of Statistical Software, 99(12), 1-31. doi:10.18637/jss.v099.i12