

The goal of bigtime is to sparsely estimate large time series models such as the Vector AutoRegressive (VAR) Model, the Vector AutoRegressive with Exogenous Variables (VARX) Model, and the Vector AutoRegressive Moving Average (VARMA) Model. The univariate cases are also supported.
You can install bigtime from github a follows:
bigtime comes with example data sets created from a VAR, VARMA and VARX DGP. These data sets are called var.example, varma.example, and varx.example respectively and can be loaded into the environment by calling data(var.example) and similarly for the others. We can have a look at the varx.example data set by first loading it into the environment and then, using a little utility function, plotting it.
library(bigtime)
suppressMessages(library(tidyverse)) # Will be used for nicer visualisations
data(varx.example) # loading the varx example data
plot_series <- function(Y){
as_tibble(Y) %>%
mutate(Time = 1:n()) %>%
pivot_longer(-Time, names_to = "Series", values_to = "vals") %>%
mutate(Series = factor(Series, levels = colnames(Y))) %>%
ggplot() +
geom_line(aes(Time, vals)) +
facet_wrap(facets = vars(Series), ncol = 1) +
ylab("") +
theme_bw()
}
plot_series(Y.varx)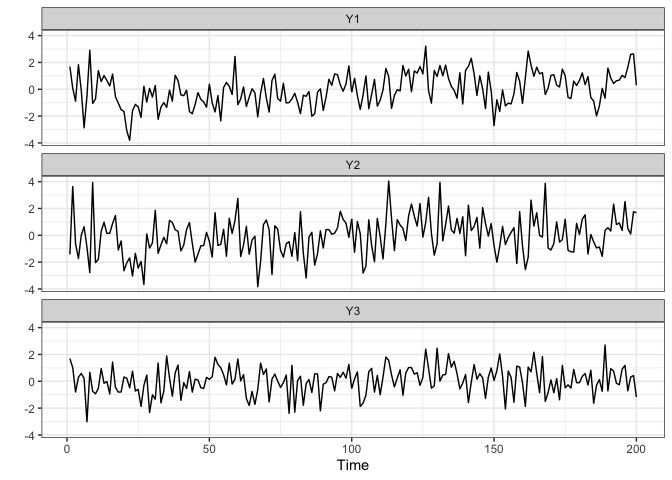

While we could use the example data provided, bigtime also supports simulation of VAR models using both lasso and elementwise type sparsity patterns. Since lasso is the most widely known one, we will start off with lasso. To simulate a VAR model having lasso type of sparsity, use the simVAR function and set sparsity_pattern="lasso". The lasso sparsity pattern has the additional num_zero option which determines the number of zeros in the VAR coefficient matrix (excluding intercepts). Note: we also set a seed so that the simulation is replicable. We can then use the summary function to obtain a summary of the simulated data.
periods <- 200 # time series length
k <- 5 # number of time series
p <- 8 # maximum lag
sparsity_options <- list(num_zero = 15) # 15 zeros across the k=5 VAR coefficient matrices
sim_data <- simVAR(periods = periods, k = k, p = p,
sparsity_pattern = "lasso",
sparsity_options = sparsity_options,
seed = 123456,
decay = 0.01) # the smaller decay the larger early coefs w.r.t. to later ones
Y.lasso <- sim_data$Y
summary(sim_data) # obtaining a summary of the simulated time series data
#> #### General Information ####
#>
#> Seed 123456
#> Time series length 200
#> Burnin 200
#> Variables Simulated 5
#> Number of Lags 8
#> Coefficients were randomly created? TRUE
#> Maximum Eigenvalue of Companion Matrix 0.8
#> Sparsity Pattern lasso
#>
#>
#> #### Sparsity Options ####
#>
#> $num_zero
#> [1] 15
#>
#>
#>
#> #### Coefficient Matrix ####
#>
#> Y1 Y2 Y3 Y4 Y5
#> Y1.L1 3.344178e-01 -1.107252e-01 -1.423944e-01 3.509198e-02 9.033998e-01
#> Y2.L1 3.347094e-01 5.264215e-01 1.003833e+00 4.685881e-01 -1.709388e-01
#> Y3.L1 -3.995565e-01 -4.468152e-01 -2.235442e-02 4.710753e-01 4.224553e-01
#> Y4.L1 2.310627e-02 -2.948322e-01 3.732432e-01 6.691342e-01 2.244958e-01
#> Y5.L1 0.000000e+00 5.040150e-01 1.543970e-02 7.602611e-02 1.855509e-01
#> Y1.L2 -1.714191e-03 6.652793e-05 2.827333e-03 3.898174e-03 -2.488847e-03
#> Y2.L2 -3.432958e-03 2.790046e-04 -4.196394e-03 -1.102596e-02 -4.531967e-03
#> Y3.L2 -3.456294e-03 6.257595e-03 4.071610e-03 4.187554e-03 -4.475995e-03
#> Y4.L2 0.000000e+00 3.882016e-03 6.860267e-04 -3.594939e-03 6.349122e-04
#> Y5.L2 -2.013360e-03 0.000000e+00 -4.561977e-04 4.355841e-03 -4.860029e-03
#> Y1.L3 -7.090490e-05 -1.972221e-05 1.289428e-05 0.000000e+00 0.000000e+00
#> Y2.L3 -1.362040e-05 -4.321743e-05 -5.979591e-05 -1.013789e-05 -4.890420e-06
#> Y3.L3 -2.603130e-05 1.255775e-05 4.926041e-06 -3.356641e-05 2.408345e-05
#> Y4.L3 -9.864658e-06 -7.407063e-06 9.288386e-07 -1.943981e-05 -2.959808e-05
#> Y5.L3 5.224473e-05 2.264257e-05 -7.240193e-05 1.758216e-05 -5.780336e-05
#> Y1.L4 3.821882e-07 -2.899947e-07 1.955819e-08 -6.271466e-07 -9.234996e-07
#> Y2.L4 4.644695e-07 -2.826756e-07 -6.312740e-07 2.079154e-07 -4.271531e-07
#> Y3.L4 1.887393e-08 3.401594e-07 1.735509e-07 2.097019e-07 0.000000e+00
#> Y4.L4 -1.992917e-07 5.054378e-07 2.266186e-07 -1.382372e-07 2.907276e-07
#> Y5.L4 3.465950e-07 1.481081e-07 6.351945e-07 2.421511e-08 5.162710e-08
#> Y1.L5 -3.412591e-09 4.406386e-09 -4.838797e-09 2.333901e-09 3.464337e-09
#> Y2.L5 3.943109e-09 -5.099138e-09 -4.262808e-12 -3.854296e-09 5.050800e-09
#> Y3.L5 -3.476037e-09 9.989383e-10 -3.456284e-10 -1.977003e-09 -1.078979e-09
#> Y4.L5 -1.601388e-09 -3.787661e-09 4.063988e-09 -1.639348e-09 -7.263552e-10
#> Y5.L5 4.748150e-09 -6.451814e-09 -9.114958e-09 -8.185059e-09 -2.599211e-09
#> Y1.L6 2.878848e-11 -4.147466e-12 0.000000e+00 -3.921230e-11 0.000000e+00
#> Y2.L6 1.757755e-12 -4.097641e-11 3.182509e-11 2.012060e-11 -6.235119e-11
#> Y3.L6 3.543788e-11 -8.333751e-12 7.345804e-11 7.110232e-12 -3.232298e-11
#> Y4.L6 7.813330e-11 4.861321e-12 -1.423732e-11 4.223140e-11 4.665353e-11
#> Y5.L6 -3.204189e-11 3.110420e-11 -8.002152e-11 -1.406136e-11 1.527682e-11
#> Y1.L7 1.035718e-13 3.868736e-13 0.000000e+00 3.274603e-14 -6.488767e-14
#> Y2.L7 5.105382e-13 -2.889064e-13 6.181295e-13 3.424112e-13 3.218496e-13
#> Y3.L7 -1.374288e-13 4.027135e-14 6.096383e-14 0.000000e+00 -1.371909e-13
#> Y4.L7 -5.274508e-13 -7.661388e-13 2.324513e-13 -6.879730e-13 0.000000e+00
#> Y5.L7 -6.332500e-13 7.399670e-13 3.913858e-13 -1.324464e-13 4.786837e-13
#> Y1.L8 -1.337775e-15 6.673161e-16 0.000000e+00 7.885634e-15 2.243677e-15
#> Y2.L8 -2.573135e-15 -1.884193e-16 4.549152e-15 1.160132e-15 1.854712e-15
#> Y3.L8 4.740580e-15 0.000000e+00 -2.501340e-15 -2.635646e-15 2.839144e-15
#> Y4.L8 0.000000e+00 -1.797436e-15 4.488466e-15 7.460492e-16 -1.452254e-15
#> Y5.L8 9.907469e-16 1.438249e-15 6.791980e-17 -9.437176e-16 0.000000e+00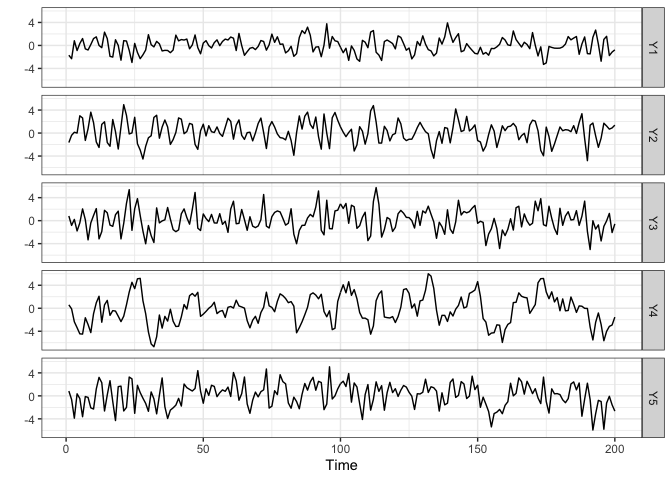
A VAR with HLag (elementwise) type of sparsity can be simulated using simVAR and by setting sparsity_pattern="HLag". Three extra options exist: (1) zero_min determines the minimum number of zero coefficients of each variable in each equation, (2) zero_max determines the maximum number of zero coefficients of each variable in each equation, and (3) zeroes_in_self is a boolean option that if TRUE, zero coefficients of the (i)th variable can exist in the (i)th equation.
periods <- 200
k <- 5 # Number of time series
p <- 5 # Maximum lag
sparsity_options <- list(zero_min = 0,
zero_max = 5,
zeroes_in_self = TRUE)
sim_data <- simVAR(periods = periods, k = k, p = p,
sparsity_pattern = "HLag",
sparsity_options = sparsity_options,
seed = 123456,
decay = 0.01)
Y.hlag <- sim_data$Y
summary(sim_data) # Obtaining a summary of the simulation
#> #### General Information ####
#>
#> Seed 123456
#> Time series length 200
#> Burnin 200
#> Variables Simulated 5
#> Number of Lags 5
#> Coefficients were randomly created? TRUE
#> Maximum Eigenvalue of Companion Matrix 0.8
#> Sparsity Pattern hvar
#>
#>
#> #### Sparsity Options ####
#>
#> $zero_min
#> [1] 0
#>
#> $zero_max
#> [1] 5
#>
#> $zeroes_in_self
#> [1] TRUE
#>
#>
#>
#> #### Coefficient Matrix ####
#>
#> Y1 Y2 Y3 Y4 Y5
#> Y1.L1 0.000000e+00 -1.032031e-01 -1.327209e-01 3.270802e-02 8.420276e-01
#> Y2.L1 3.119710e-01 4.906592e-01 9.356382e-01 4.367547e-01 -1.593261e-01
#> Y3.L1 -3.724128e-01 -4.164610e-01 -2.083578e-02 4.390729e-01 3.937560e-01
#> Y4.L1 2.153655e-02 -2.748029e-01 3.478871e-01 0.000000e+00 2.092447e-01
#> Y5.L1 -2.818808e-01 4.697750e-01 1.439081e-02 7.086130e-02 1.729456e-01
#> Y1.L2 0.000000e+00 0.000000e+00 2.635259e-03 3.633353e-03 -2.319768e-03
#> Y2.L2 -3.199742e-03 2.600505e-04 0.000000e+00 -1.027691e-02 -4.224090e-03
#> Y3.L2 -3.221492e-03 5.832487e-03 0.000000e+00 3.903074e-03 -4.171920e-03
#> Y4.L2 0.000000e+00 3.618292e-03 6.394217e-04 0.000000e+00 5.917797e-04
#> Y5.L2 -1.876583e-03 -3.611195e-03 -4.252061e-04 4.059929e-03 -4.529864e-03
#> Y1.L3 0.000000e+00 0.000000e+00 1.201831e-05 0.000000e+00 5.747130e-05
#> Y2.L3 -1.269510e-05 -4.028146e-05 0.000000e+00 -9.449180e-06 -4.558191e-06
#> Y3.L3 -2.426287e-05 1.170464e-05 0.000000e+00 -3.128609e-05 2.244735e-05
#> Y4.L3 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 -2.758734e-05
#> Y5.L3 0.000000e+00 2.110436e-05 -6.748333e-05 1.638772e-05 -5.387651e-05
#> Y1.L4 0.000000e+00 0.000000e+00 1.822951e-08 0.000000e+00 -8.607620e-07
#> Y2.L4 4.329159e-07 -2.634722e-07 0.000000e+00 0.000000e+00 -3.981346e-07
#> Y3.L4 0.000000e+00 3.170507e-07 0.000000e+00 1.954558e-07 -9.491777e-08
#> Y4.L4 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> Y5.L4 0.000000e+00 1.380464e-07 5.920428e-07 0.000000e+00 4.811983e-08
#> Y1.L5 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 3.228988e-09
#> Y2.L5 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> Y3.L5 0.000000e+00 0.000000e+00 0.000000e+00 -1.842696e-09 -1.005678e-09
#> Y4.L5 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> Y5.L5 0.000000e+00 -6.013512e-09 -8.495736e-09 0.000000e+00 0.000000e+00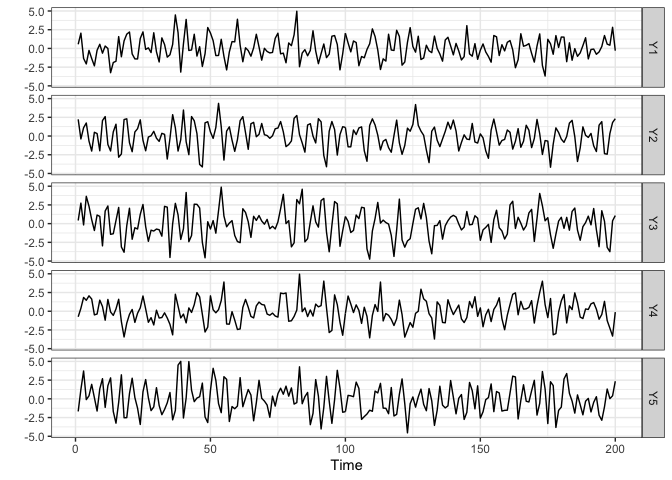
The above simulated data (and truly any other data) could then be estimated using an L1-penalty (lasso penalty) on the autoregressive coefficients. To this end, set the VARpen argument in the sparseVAR function equal to L1. Note: it is recommended to standardise the data. Bigtime will give a warning if the data is not standardised but will not stop you from continuing. Setting selection="none", the default, allows us to specify the penalization we want. Furthermore, we can predefine the maximum lag-order by changing the p argument to the desired value. However, we do not recommend this, as the bigtime will, by default, choose a maximum lag-order that is well suited in many scenarios.
VAR.L1 <- sparseVAR(Y = scale(Y.lasso), # standardising the data
VARpen = "L1", # using lasso penalty
VARlseq = 1.5) # Specifying the penalty to be used. selection="none" is the default.For the selection of the penalization parameter, we can either set the selection argument to "none", which would return a model for a sequence of penalizations, or use time series cross-validation by setting selection="cv", or finally we could also use any of BIC, AIC, or HQ information criteria by setting the selection arguments to any of "bic", "aic", or "hq" respectively. We will start of by using time series cross-validation and will therefore set selection="cv". The default is to use a cross-validation score based on one-step ahead predictions but you can change the default forecast horizon under the argument h.
VAR.L1 <- sparseVAR(Y=scale(Y.lasso), # standardising the data
selection = "cv", # using time series cross-validation
VARpen = "L1") # using the lasso penaltyThe plot_cv function can be used to investigate the cross-validation procedure. The returned plot shows the mean MSFE for each penalization together with error bars for plus-minus one standard deviation. The black dashed line indicates the penalty parameter choice that lead to the smallest MSFE in the CV procedure. The red dotted line, on the other hand, shows the one-standard-error solution. It picks the most parsimonious model within one standard error of the best cross-validation score. The latter is the one that is chosen by default in sparseVAR.
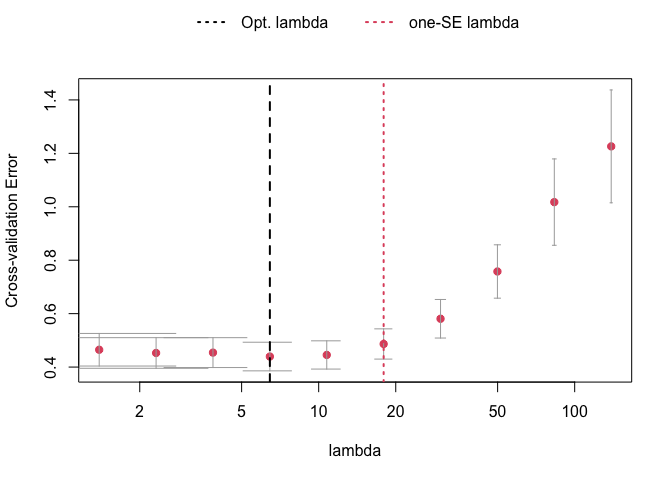
Further investigation into the model can be done by using the function lagmatrix, which returns the lagmatrix of the estimated autoregressive coefficients. If entry ((i,j)=x), this means that the sparse estimator indicates the effect of time series (j) on time series (i) to last for (x) periods. Setting the returnplot argument to TRUE will return a heatmap for better visual inspection.
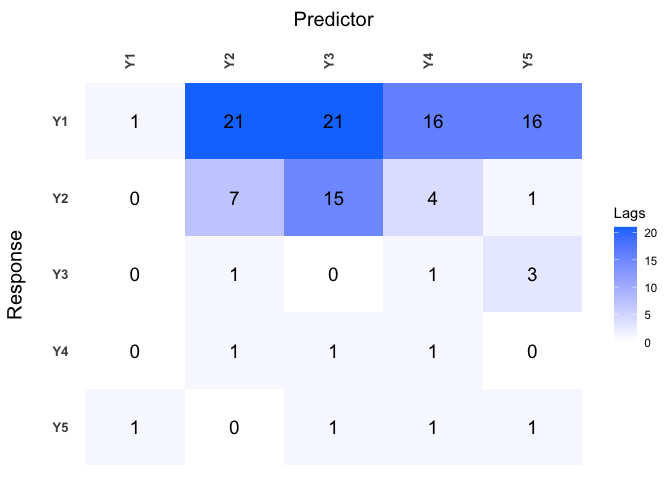
The lag matrix is typically sparse as it contains some empty (i.e., zero) cells. However, VAR models estimated with a standard L1-penalty are typically not easily interpretable as they select many high lag order coefficients (i.e., large values in the lagmatrix).
To circumvent this problem, we advise using a lag-based hierarchically sparse estimation procedure, which boils down to using the default option HLag for the VARpen argument. This estimation procedure encourages low maximum lag orders, often results in sparser lagmatrices, and hence more interpretable models.
Models can be estimated using the hierarchical penalization by using the default argument to VARpen, namely HLag. Model selection can again be done by either setting selection="none" and obtaining a whole sequence of models, or by using any of cv, bic, aic, hq.
VARHLag_none <- sparseVAR(Y=scale(Y.hlag),
selection = "none") # HLag is the default VARpen option
VARHLag_cv <- sparseVAR(Y=scale(Y.hlag),
selection = "cv")
VARHLag_bic <- sparseVAR(Y=scale(Y.hlag),
selection = "bic") # This will also give a table for IC comparison showing the selected lambda for each IC
#>
#>
#> #### Selected the following lambda ####
#>
#> AIC BIC HQ
#> 10.74023 10.74023 10.74023
#>
#>
#> #### Details ####
#>
#> lambda AIC BIC HQ
#> 1 138.7154 -0.9793 -0.9793 -0.9793
#> 2 83.1577 -1.7792 -1.6473 -1.7258
#> 3 49.8517 -3.0055 -2.7746 -2.912
#> 4 29.8853 -4.1453 -3.8155 -4.0118
#> 5 17.9158 -4.826 -4.4631 -4.6791
#> 6 10.7402 ==> -5.0769 ==> -4.6151 ==> -4.89
#> 7 6.4386 -5.0698 -4.3277 -4.7695
#> 8 3.8598 -4.6703 -3.0377 -4.0096
#> 9 2.3139 -2.7531 2.5737 -0.5974
#> 10 1.3872 -1.5512 6.5956 1.7457Depending on which selection procedure was used, various diagnostics can be produced. Former and foremost, all selection procedures support the fitted and residuals functions to obtain the fitted and residual values respectively. Both functions return a 3D array if the model used selection="none" corresponding to the fitted/residual values for each model in the penalization sequence.
res_VARHLag_none <- residuals(VARHLag_none) # This is a 3D array
dim(res_VARHLag_none)
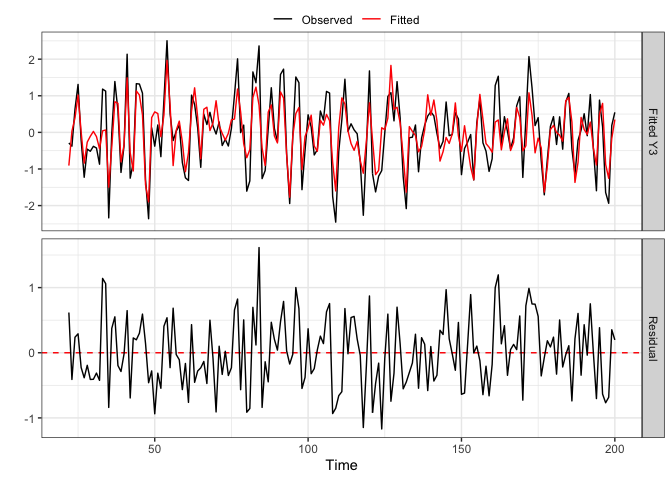
#> [1] 179 5 10When an actual selection method was used (cv, bic, aic, hq), then other diagnostic functions exist. For cv, plot_cv could be used again, just as shown above. For all, the diagnostics_plot function can be used to obtain a plot of fitted and residual values.
p_bic <- diagnostics_plot(VARHLag_bic, variable = "Y3") # variable argument can be numeric or character
p_cv <- diagnostics_plot(VARHLag_cv, variable = "Y3") # variable argument can be numeric or character
plot(p_bic)
Often practitioners are interested in incorporating the impact of unmodeled exogenous variables (X) into the VAR model. To do this, you can use the sparseVARX function which has an argument X where you can enter the data matrix of exogenous time series. For demonstration purposes, we will use the varx.example data set that is part of bigtime.
When applying the lagmatrix function to an estimated sparse VARX model, the lag matrices of both the endogenous and exogenous autoregressive coefficients are returned.
sparseVARX supports the same selection arguments as sparseVAR: none, cv, bic, aic, hq, and it is again recommended to standardise the data.
VARXfit_cv <- sparseVARX(Y=scale(Y.varx), X=scale(X.varx), selection = "cv")
LhatVARX <- lagmatrix(fit=VARXfit_cv, returnplot=TRUE)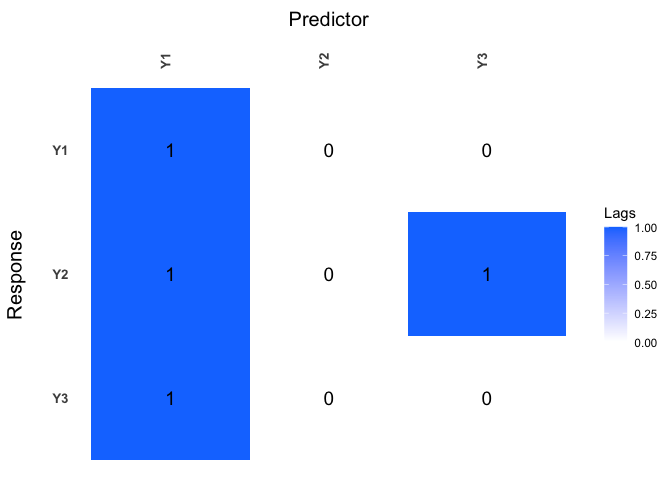

VARX models also support plot_cv if estimated using CV. The returned plot shows the mean MSFE for each combination of penalizations in a heatmap. The x-axis show the penalizations for the exogenous variables, and the y-axis shows the penalizations for the endogenous variables. The big black dot in the plot below indicates the one-SE optimal choice, while the contours indicate the mean MSFE in the CV procedure. The red colour indicates a high MSFE, and light-yellow to yellow regions indicate low MSFEs.

If selection="none" a 3D array will be returned again. Although not mentioned previously, when setting selection to none, or any of the IC, one can also easily provide a penalization sequence, or even just ask for a single penalization setting. For example, below we intentionally choose a single, small penalization for the exogenous variables.
VARXfit_none <- sparseVARX(Y=scale(Y.varx), X=scale(X.varx), VARXlBseq = 0.001, selection = "none")
dim(VARXfit_none$Phihat) # This is a 3D array
#> [1] 3 63 10
# This is also 3D but third dimension is equal to ten
# --> one penalization was chosen for B and 10 automatically for Phi
# --> Cross product makes 10
dim(VARXfit_none$Bhat)
#> [1] 3 63 10Other functions such as residuals, fitted, and diagnostics_plot are also supported.
VARMA models generalise VAR models and often allow for more parsimonious representations of the data generating process. To estimate a VARMA model to a multivariate time series data set, use the function sparseVARMA, and choose a desired selection method. The sparse VARMA estimation procedures consists of two stages: in the first stage a VAR model is estimated from which the residuals are retrieved. In the second stage these residuals are used as approximated error terms to estimate the VARMA model. As a default, sparseVARMA uses CV in the first stage and none in the second stage. The first stage does not support none: A selection needs to be made.
Now lag matrices are obtained for the autoregressive (AR) coefficients and the moving average (MAs) coefficients.
data(varma.example)
VARMAfit <- sparseVARMA(Y=scale(Y.varma), VARMAselection = "cv") # VARselection="cv" as default.
LhatVARMA <- lagmatrix(fit=VARMAfit, returnplot=T)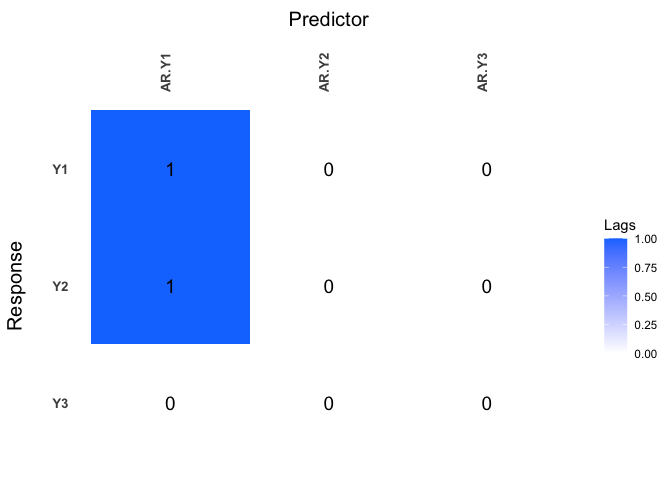
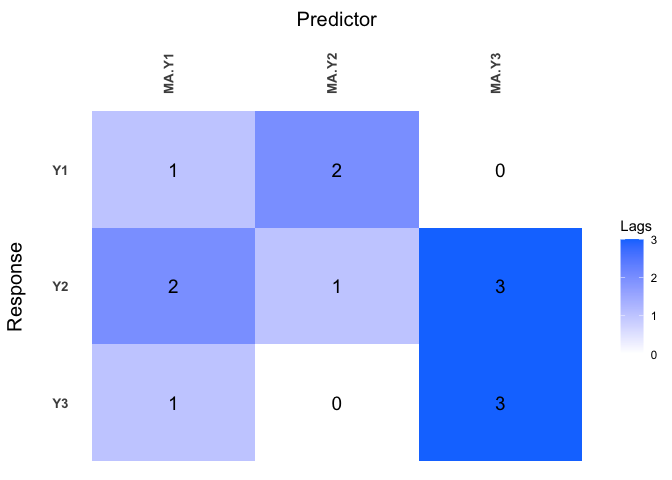
Other functions such as plot_cv, residuals, fitted and diagnosticsplot are also supported.
To obtain forecasts from the estimated models, you can use the directforecast function for VAR, VARMA, and VARX, or the recursiveforecast function for VAR models. The default forecast horizon (argument h) is set to one such that one-step ahead forecasts are obtained, but you can specify your desired forecast horizon.
Finally, we compare the forecast accuracy of the different models by comparing their forecasts to the actual time series values of the var.example data set that comes with bigtime. We will estimate all models using CV.
In this example, the VARMA model has the best forecast performance (i.e., lowest mean squared prediction error). This is somewhat surprising given the data comes from a VAR model.
data(var.example)
dim(Y.var)
#> [1] 200 5
Y <- Y.var[-nrow(Y.var), ] # leaving the last observation for comparison
Ytest <- Y.var[nrow(Y.var), ]
VARcv <- sparseVAR(Y = scale(Y), selection = "cv")
VARMAcv <- sparseVARMA(Y = scale(Y), VARMAselection = "cv")
Y <- Y.var[-nrow(Y.var), 1:3] # considering first three variables as endogenous
X <- Y.var[-nrow(Y.var), 4:5] # and last two as exogenous
VARXcv <- sparseVARX(Y = scale(Y), X = scale(X), selection = "cv")
VARf <- directforecast(VARcv) # default is h=1
VARXf <- directforecast(VARXcv)
VARMAf <- directforecast(VARMAcv)
# We can only compare forecasts for the first three variables
# because VARX models only forecast endogenously modelled variables
mean((VARf[1:3]-Ytest[1:3])^2)
#> [1] 0.6252039
mean((VARXf[1:3]-Ytest[1:3])^2)
#> [1] 0.6319843
mean((VARMAf[1:3]-Ytest[1:3])^2) # lowest=best
#> [1] 0.4571325Note that we could easily obtain longer horizon forecasts for the VAR model by using the recursiveforecast function. It is recommended to call is.stable first though, to check whether the obtained VAR model is stable.
is.stable(VARcv)
#> [1] TRUE
rec_fcst <- recursiveforecast(VARcv, h = 10)
plot(rec_fcst, series = "Y2", last_n = 50) # Plotting of a recursive forecast
The functions sparseVAR, sparseVARX, sparseVARMA can also be used for the univariate setting where the response time series (Y) is univariate. Below we illustrate the usefulness of the sparse estimation procedure as automatic lag selection procedures.
We start by generating a time series of length (n=50) from a stationary AR model and by plotting it. The sparseVAR function can also be used in the univariate case as it allows the argument Y to be a vector.
The lagmatrix function gives the selected autoregressive order of the sparse AR model. The true order is one.
periods <- 50
k <- 1
p <- 1
sim_data <- simVAR(periods, k, p,
sparsity_pattern = "none",
max_abs_eigval = 0.5,
seed = 123456)
summary(sim_data)
#> #### General Information ####
#>
#> Seed 123456
#> Time series length 50
#> Burnin 50
#> Variables Simulated 1
#> Number of Lags 1
#> Coefficients were randomly created? TRUE
#> Maximum Eigenvalue of Companion Matrix 0.5
#> Sparsity Pattern none
#>
#>
#> #### Sparsity Options ####
#>
#> NULL
#>
#>
#> #### Coefficient Matrix ####
#>
#> [,1]
#> [1,] 0.4998982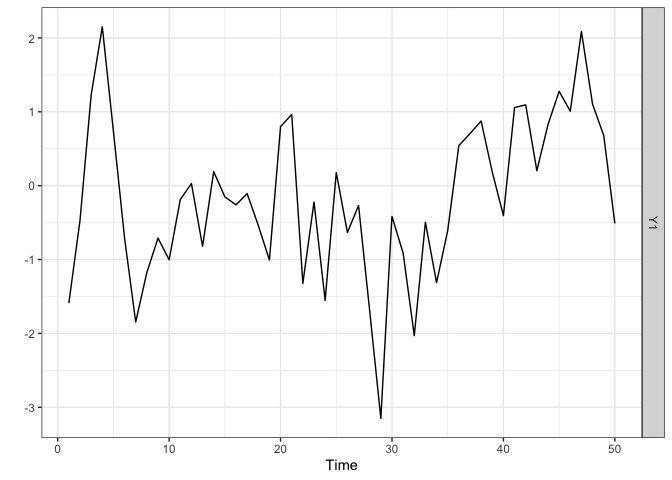
y <- scale(sim_data$Y)
ARfit <- sparseVAR(Y=y, selection = "cv")
lagmatrix(ARfit)
#> $LPhi
#> [,1]
#> [1,] 1Note that all diagnostics functions discussed for the VAR, VARMA, VARX cases also work for univariate cases; so do the forecasting functions.
We start by generating a time series of length (n=50) from a stationary ARX model and by plotting it. The sparseVARX function can also be used in the univariate case as it allows the arguments Y and X to be vectors. The lagmatrix function gives the selected endogenous (under LPhi) and exogenous autoregressive (under LB) orders of the sparse ARX model. The true orders are one.
periods <- 50
k <- 1
p <- 1
burnin <- 100
Xsim <- simVAR(periods+burnin+1, k, p, max_abs_eigval = 0.8, seed = 123)
edist <- lag(Xsim$Y)[-1, ] + rnorm(periods + burnin, sd = 0.1)
Ysim <- simVAR(periods, k , p, max_abs_eigval = 0.5, seed = 789,
e_dist = t(edist), burnin = burnin)
plot(Ysim)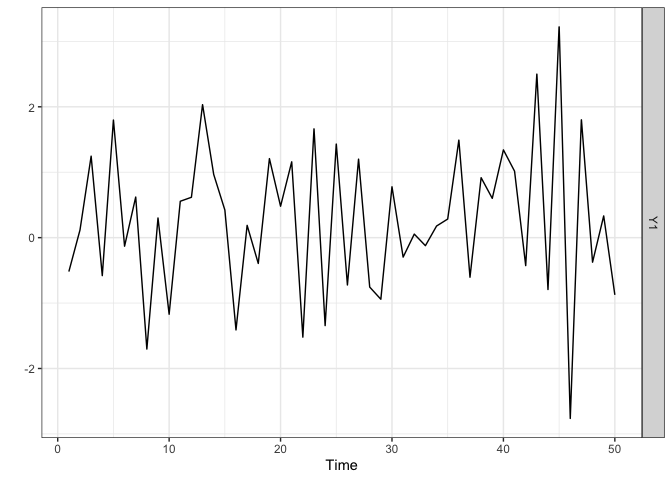
x <- scale(Xsim$Y[-(1:(burnin+1))])
y <- scale(Ysim$Y)
ARXfit <- sparseVARX(Y=y, X=x, selection = "cv")
lagmatrix(fit=ARXfit)
#> $LPhi
#> [,1]
#> [1,] 1
#>
#> $LB
#> [,1]
#> [1,] 2We start by generating a time series of length (n=50) from a stationary ARMA model and by plotting it. The sparseVARMA function can also be used in the univariate case as it allows the argument Y to be a vector. The lagmatrix function gives the selected autoregressive (under LPhi) and moving average (under LTheta) orders of the sparse ARMA model. The true orders are one.
periods <- 50
k <- 1
p.u <- 1
p.y <- 1
burnin <- 100
u <- rnorm(periods + 1 + burnin, sd = 0.1)
u <- embed(u, dimension = p.u + 1)
u <- u * matrix(rep(c(1, 0.2), nrow(u)), nrow = nrow(u), byrow = TRUE) # Second column is lagged, first is current error
edist <- rowSums(u)
Ysim <- simVAR(periods, k, p, e_dist = t(edist),
max_abs_eigval = 0.5, seed = 789,
burnin = burnin)
summary(Ysim)
#> #### General Information ####
#>
#> Seed 789
#> Time series length 50
#> Burnin 100
#> Variables Simulated 1
#> Number of Lags 1
#> Coefficients were randomly created? TRUE
#> Maximum Eigenvalue of Companion Matrix 0.5
#> Sparsity Pattern none
#>
#>
#> #### Sparsity Options ####
#>
#> NULL
#>
#>
#> #### Coefficient Matrix ####
#>
#> [,1]
#> [1,] 0.4989384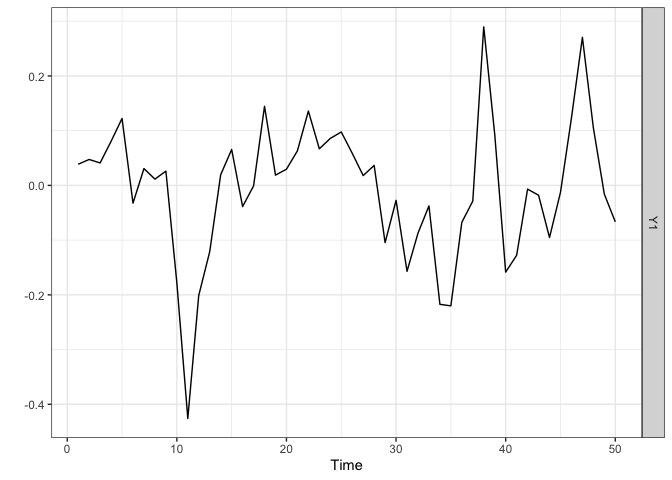
ARMAfit <- sparseVARMA(Y=y, VARMAselection = "cv")
lagmatrix(fit=ARMAfit)
#> $LPhi
#> [,1]
#> [1,] 3
#>
#> $LTheta
#> [,1]
#> [1,] 0For a non-technical introduction to VAR models see this interactive notebook and for an interactive notebook demonstrating the use of bigtime for high-dimensional VARs, see this notebook. Note: Loading these notebooks sometimes can take quite some time. Please be patient or try another time.
Nicholson William B., Wilms Ines, Bien Jacob and Matteson David S. (2020), “High-dimensional forecasting via interpretable vector autoregression”, Journal of Machine Learning Research, 21(166), 1-52.
Wilms Ines, Basu Sumanta, Bien Jacob and Matteson David S. (2021), “Sparse Identification and Estimation of Large-Scale Vector AutoRegressive Moving Averages”, Journal of the American Statistical Association, doi: 10.1080/01621459.2021.1942013.
Wilms Ines, Basu Sumanta, Bien Jacob and Matteson David S. (2017), “Interpretable Vector AutoRegressions with Exogenous Time Series”, NIPS 2017 Symposium on Interpretable Machine Learning, arXiv:1711.03623