
NEW! Try the online app for visualising IBD distributions: ibdsim2-shiny
The purpose of ibdsim2 is to simulate and analyse the gene flow in pedigrees. In particular, such simulations can be used to study distributions of chromosomal segments shared identical-by-descent (IBD) by pedigree members. In each meiosis, the recombination process is simulated using sex specific recombination rates in the human genome (Halldorsson et al., 2019), or with recombination maps provided by the user. Additional features include calculation of realised relatedness coefficients, distribution plots of IBD segments, and estimation of two-locus relatedness coefficients.
ibdsim2 is part of the ped suite collection of packages for pedigree analysis in R. A detailed presentation of these packages, including a separate chapter on ibdsim2, is available in the book Pedigree analysis in R (Vigeland, 2021).
To get ibdsim2, install from CRAN as follows:
install.packages("ibdsim2")Alternatively, the latest development version can be installed from GitHub:
# install.packages("devtools") # if needed
devtools::install_github("magnusdv/ibdsim2")The most important function in ibdsim2 is
ibdsim(), which simulates the recombination process in a
given pedigree. In this example we demonstrate this for in a family
quartet, and show how to visualise the result.
We start by loading ibdsim2.
library(ibdsim2)The main input to ibdsim() is a pedigree and a
recombination map. In our case we use
pedtools::nuclearPed() to create the pedigree, and we load
chromosome 1 of the built-in map of human recombination.
# Pedigree with two siblings
x = nuclearPed(2)
# Recombination map
chr1 = loadMap("decode19", chrom = 1)Now run the simulation! The seed argument ensures
reproducibility.
sim = ibdsim(x, N = 1, map = chr1, seed = 1234, verbose = F)The output of ibdsim() is a list of length
N (the number of simulations), where each simulation result
is contained in matrix form. Here are the first few rows of the single
simulation we just made:
head(sim[[1]])
#> chrom start end length 1:p 1:m 2:p 2:m 3:p 3:m 4:p 4:m
#> [1,] 1 1.431813 6.386532 4.9547193 1 2 3 4 2 4 2 4
#> [2,] 1 6.386532 19.733718 13.3471854 1 2 3 4 2 4 2 3
#> [3,] 1 19.733718 20.220621 0.4869035 1 2 3 4 1 4 2 3
#> [4,] 1 20.220621 58.236210 38.0155893 1 2 3 4 1 4 2 4
#> [5,] 1 58.236210 59.425280 1.1890698 1 2 3 4 1 3 2 4
#> [6,] 1 59.425280 82.385463 22.9601825 1 2 3 4 1 3 2 3Each row of the matrix corresponds to a segment of the genome, and describes the allelic state of the pedigree in that segment. Each individual has two columns, one with the paternal allele (marked by the suffix “:p”) and one with the maternal (suffix “:m”). The founders (the parents in our case) are assigned alleles 1, 2, 3 and 4.
The function haploDraw() interprets the alleles 1-4 as
colours and draws the resulting haplotypes onto the pedigree. See
?haploDraw for explanation of the arguments.
haploDraw(x, sim[[1]], pos = c(2, 4, 1, 1), cols = c(3, 7, 2, 4),
margin = c(6, 4, 3, 4))
In this example we will compare the distributions of counts/lengths of IBD segments between the following pairwise relationships:
Note that GR and HS have the same relatedness coefficients
kappa = (1/2, 1/2, 0), meaning that they are genetically
indistinguishable in the context of unlinked loci. In contrast, HU has
kappa = (3/4, 1/4, 0).
For simplicity we create a pedigree containing all the three relationships we are interested in.
x = addSon(halfSibPed(), parent = 5)
plot(x)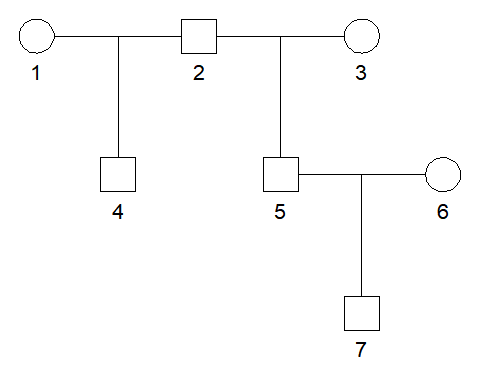
We store the ID labels of the three relationships in a list.
ids = list(GR = c(2,7),
HS = 4:5,
HU = c(4,7))Next, we use ibdsim() to produce 500 simulations of the
underlying IBD pattern in the entire pedigree.
s = ibdsim(x, N = 500, map = "decode19", seed = 1234)
#> Simulation parameters:
#> Simulations : 500
#> Chromosomes : 1-22
#> Genome length: 2753.93 Mb
#> 2602.29 cM (male)
#> 4180.42 cM (female)
#> Recomb model : chi
#> Target indivs: 1-7
#> Skip recomb : -
#> Total time used: 11.4 secsThe plotSegmentDistribution() function, with the option
type = "ibd1" analyses the IBD segments in each simulation,
and makes a nice plot. Note that the names of the ids list
are used in the legend.
plotSegmentDistribution(s, type = "ibd1", ids = ids, shape = 1:3)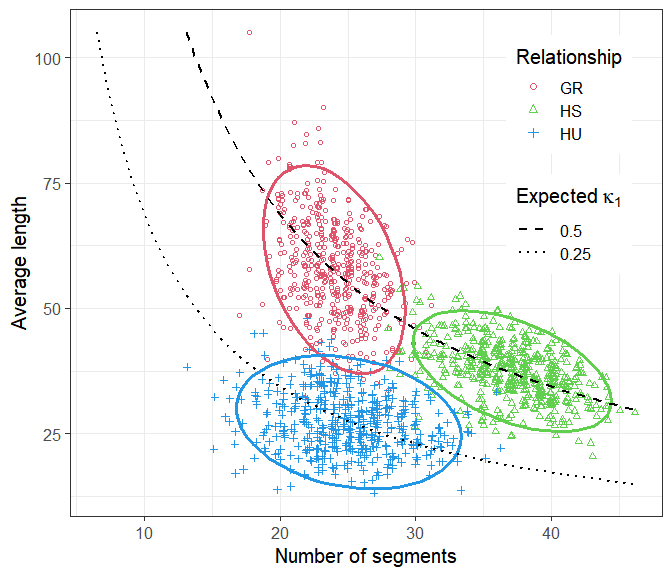
We conclude that the three distributions are almost completely disjoint. In particular, GR and HS are separable on the basis of their IBD segments, if these can be determined accurately enough.
A Shiny app for visualising IBD distributions is now available here: https://magnusdv.shinyapps.io/ibdsim2-shiny/.