

The primary goal of metapower is to compute statistical power for meta-analyses. Currently, metapower has the following functionality:
Computation of statistical power for:
metapower can currently handle the following designs and effect sizes:
You can install the released version of metapower from CRAN with:
And the development version from GitHub with:
Check out the simple and easy to use shiny application
library(metapower)
my_power <- mpower(effect_size = .3, study_size = 20, k = 10, i2 = .50, es_type = "d")
print(my_power)
#>
#> Power Analysis for Meta-analysis
#>
#> Effect Size Metric: d
#> Expected Effect Size: 0.3
#> Expected Study Size: 20
#> Expected Number of Studies: 10
#>
#> Estimated Power: Mean Effect Size
#>
#> Fixed-Effects Model 0.5594533
#> Random-Effects Model (i2 = 50%): 0.3454424
plot_mpower(my_power)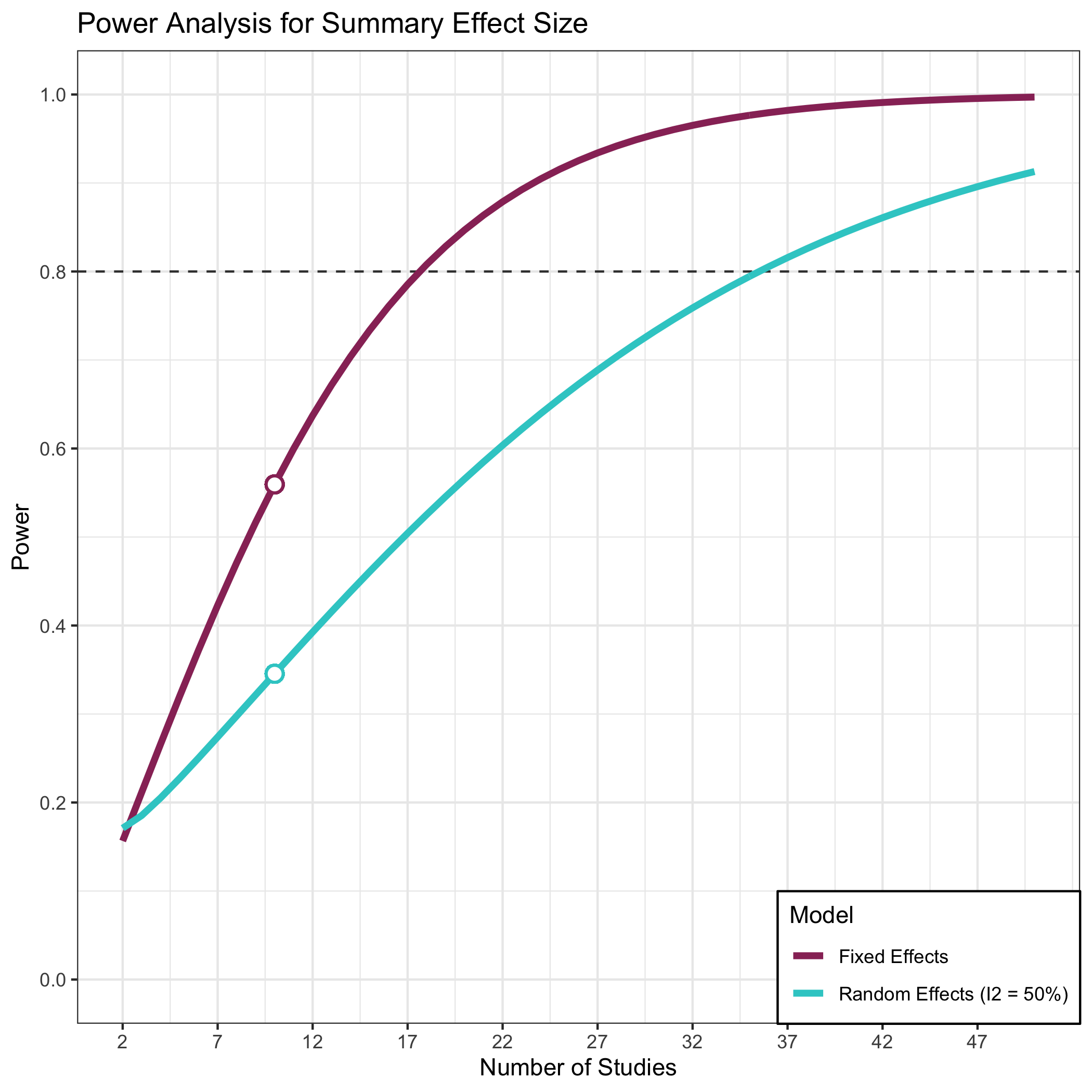
See Vignette “Using metapower” for more information..
All mathematical calculations are derived from Hedges & Pigott (2004), Bornstein, Hedges, Higgins, & Rothstein (2009),Pigott (2012), Jackson & Turner (2017).
Bornstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2009). Introduction to meta-analysis. Hoboken, NJ: Wiley.
Hedges, L. V., & Pigott, T. D. (2004). The power of statistical tests for moderators in meta-analysis. Psychological Methods, 9(4), 426–445. https://doi.org/10.1037/1082-989x.9.4.426
Jackson, D., & Turner, R. (2017). Power analysis for random‐effects meta-analysis. Research Synthesis Methods, 8(3), 290–302. https://doi.org/10.1002/jrsm.1240
Pigott, T. D. (2012). Advances in meta-analysis. NewYork, NY: Springer.
If you encounter a clear bug, please file a minimal reproducible example on github.