pedprobr

Introduction

The main content of pedprobr is an implementation of the Elston-Stewart algorithm for pedigree likelihoods. It is a reboot of the implementation in paramlink which is no longer actively developed.

pedprobr is part of the ped suite, a collection of packages for pedigree analysis in R, based on pedtools for basic handling of pedigrees and marker data. In particular, pedprobr does much of the hard work in the forrel package for relatedness analysis and forensic pedigree analysis.

The workhorse of the pedprobr package is the likelihood() function, which works in a variety of situations:

• complex inbred pedigrees
• pedigrees with inbred founders
• autosomal and X-linked markers
• a single marker or two linked markers
• markers with mutation models (supported by pedmut)

Installation

To get the current official version of pedprobr, install from CRAN as follows:

install.packages("pedprobr")

Alternatively, you can obtain the latest development version from GitHub:

# install.packages("devtools") # install devtools if needed
devtools::install_github("magnusdv/pedprobr")

Getting started

library(pedprobr)
#> Loading required package: pedtools

To set up a simple example, we first use pedtools utilities to create a pedigree with a single attached marker object. The marker has alleles a and b, with frequencies 0.2 and 0.8 respectively, and both brothers are heterozygous.

# Pedigree
x = nuclearPed(nch = 2)

# Add a single marker
x = addMarker(x, geno = c(NA, NA, "a/b", "a/b"), afreq = c(a = 0.2, b = 0.8))

# Plot with genotypes
plot(x, marker = 1)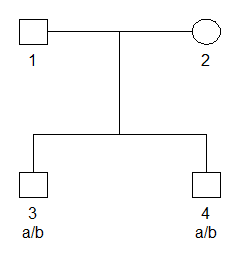

The pedigree likelihood, i.e., the probability of the genotypes given the pedigree, is obtained as follows:

likelihood(x, marker = 1)
#> [1] 0.1856

Genotype probability distributions

Besides likelihood(), other important functions in pedprobr are:

• oneMarkerDistribution() : the joint genotype distribution at a single marker, for any subset of pedigree members
• twoMarkerDistribution() : the joint genotype distribution at two linked markers, for a single person

In both cases, the distributions are computed conditionally on any known genotypes at the markers in question.

To illustrate oneMarkerDistribution() we continue our example from above, and consider the following question: What is the joint genotype distribution of the parents, conditional on the genotypes of the children?

The answer is found as follows:

oneMarkerDistribution(x, ids = 1:2, partialmarker = 1, verbose = F)
#>            a/a        a/b       b/b
#> a/a 0.00000000 0.01724138 0.1379310
#> a/b 0.01724138 0.13793103 0.2758621
#> b/b 0.13793103 0.27586207 0.0000000

For example, the output confirms the intuitive result that the parents cannot both be homozygous for the same allele. The most likely combination is that one parent is heterozygous a/b, while the other is homozygous b/b.