Authors: Ludvig R. Olsen ( r-pkgs@ludvigolsen.dk )
License: MIT
Started: April 2020
Rearrrange Data
Authors: Ludvig R.
Olsen (
r-pkgs@ludvigolsen.dk
)
License: MIT
Started: April 2020
R package for rearranging data by a set of methods.
We distinguish between rearrangers and mutators, where the first reorders the data points and the second changes the values of the data points.
When performing an operation relative to a point in an n-dimensional
vector space, we refer to the point as the origin. If
we, for instance, wish to rotate our data points around the point at
x = 3 and y = 7, those are the coordinates of
our origin.
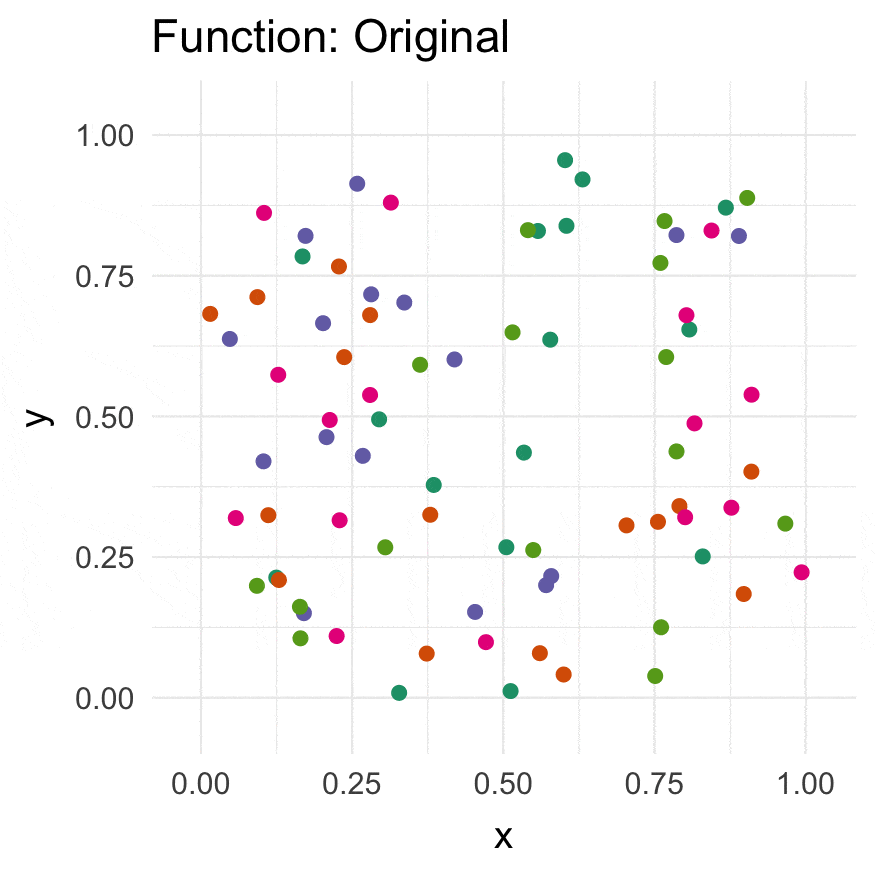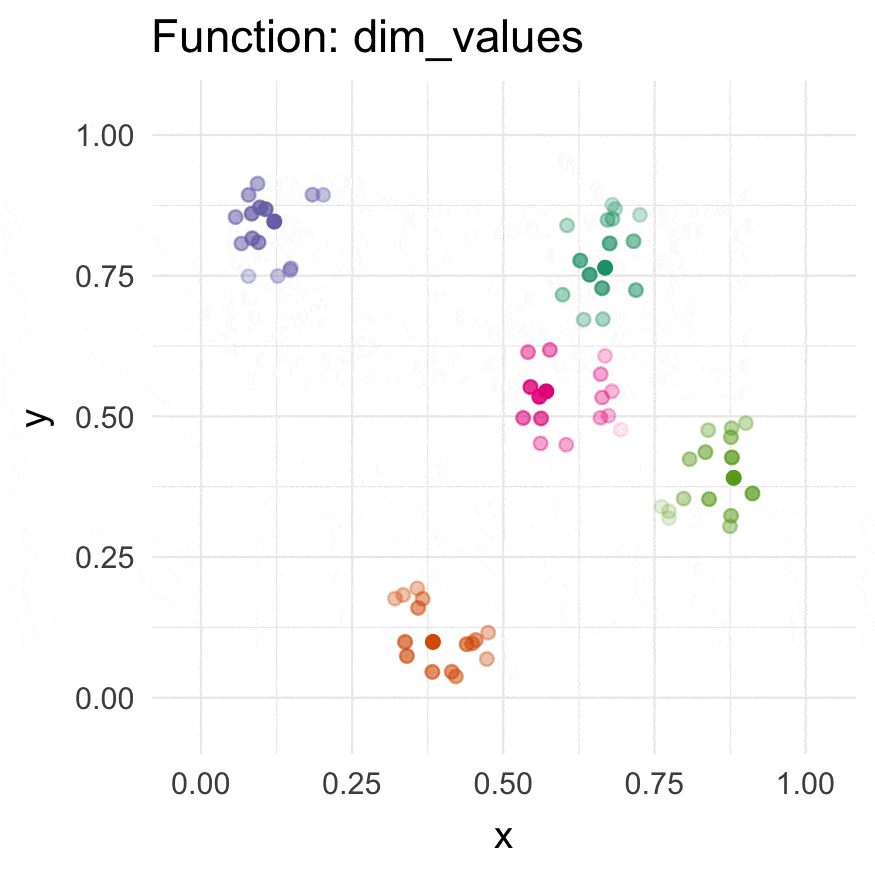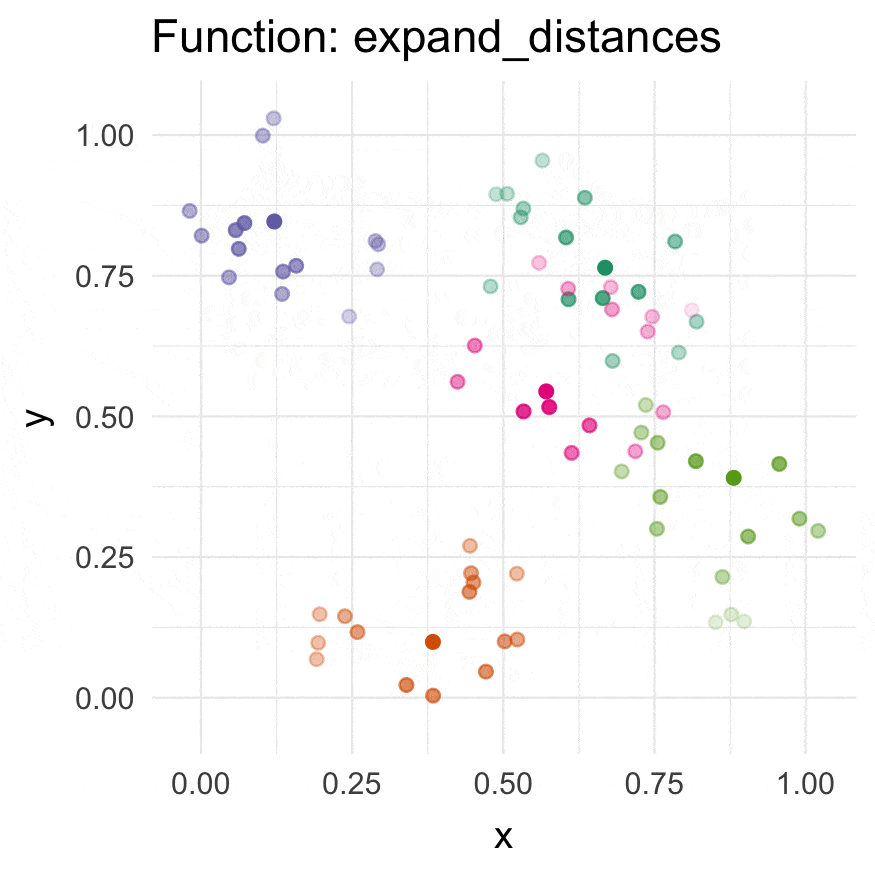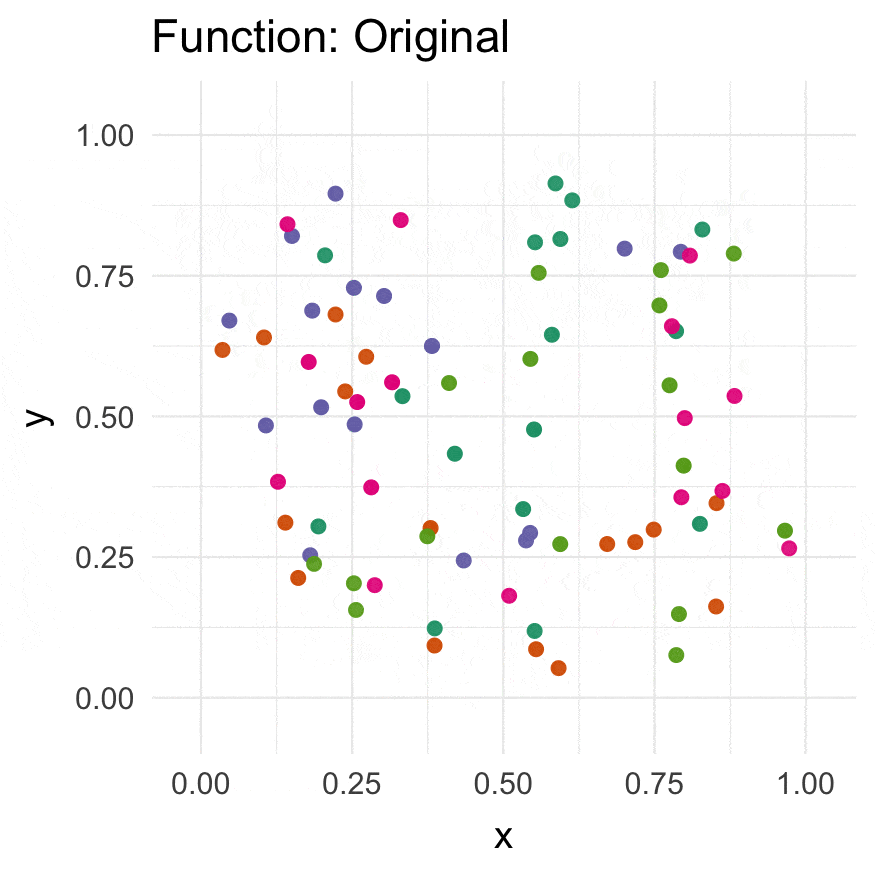
CRAN (when available):
install.packages("rearrr")
Development version:
install.packages("devtools")
devtools::install_github("LudvigOlsen/rearrr")
| Function | Description |
|---|---|
center_max() |
Center the highest value with values decreasing around it. |
center_min() |
Center the lowest value with values increasing around it. |
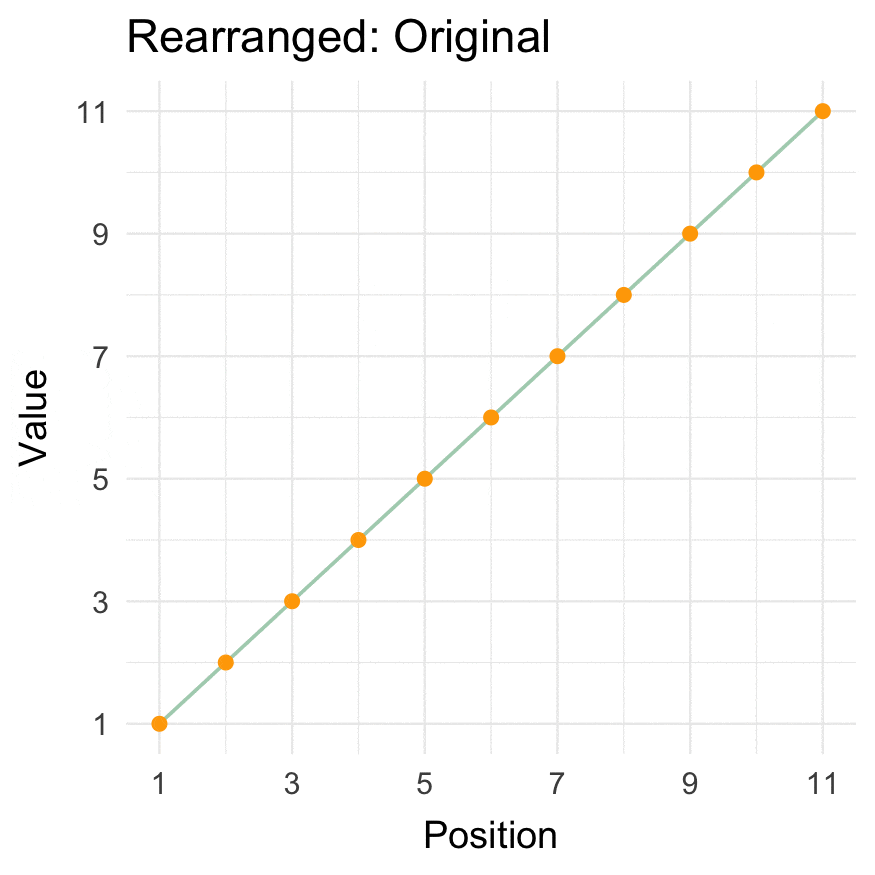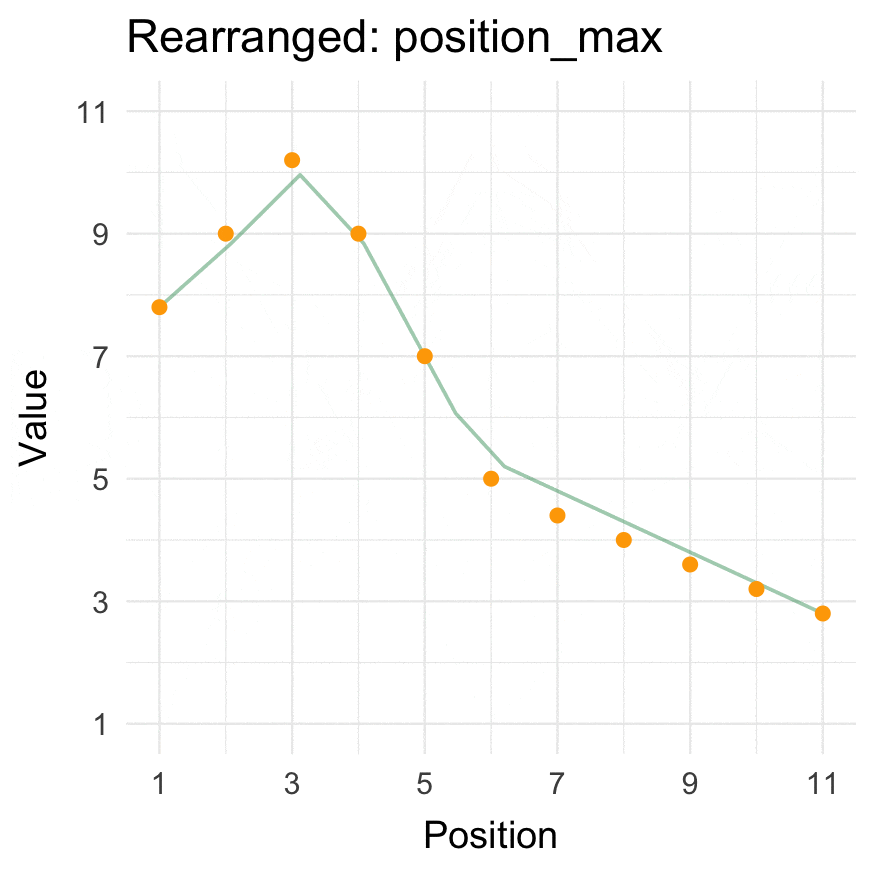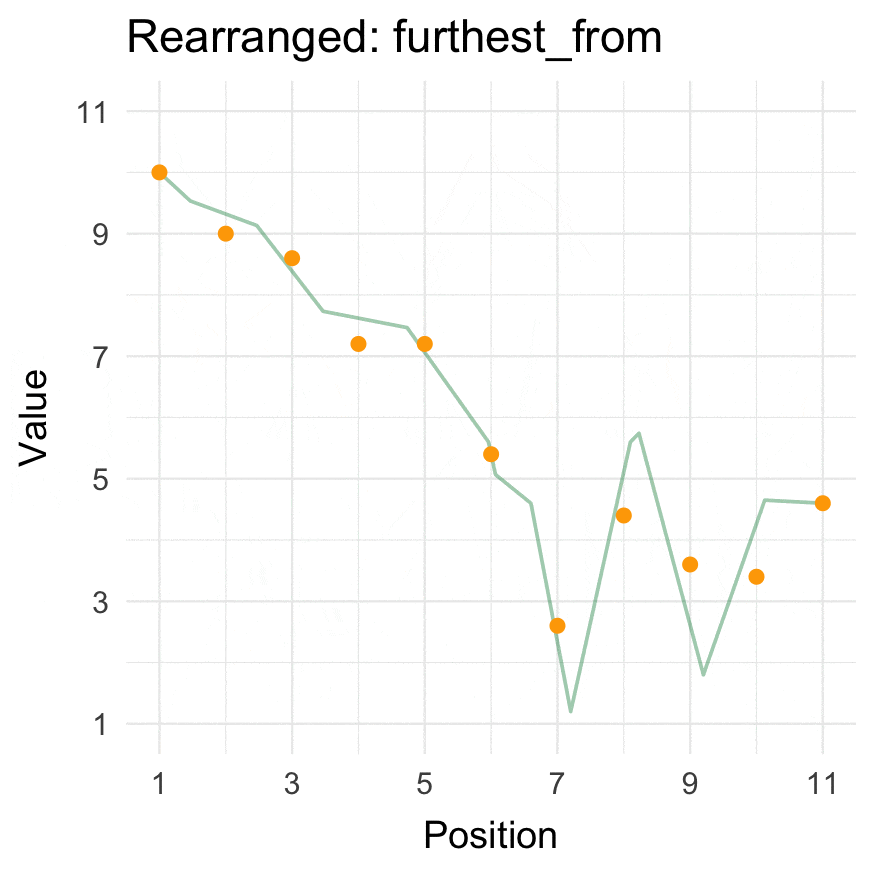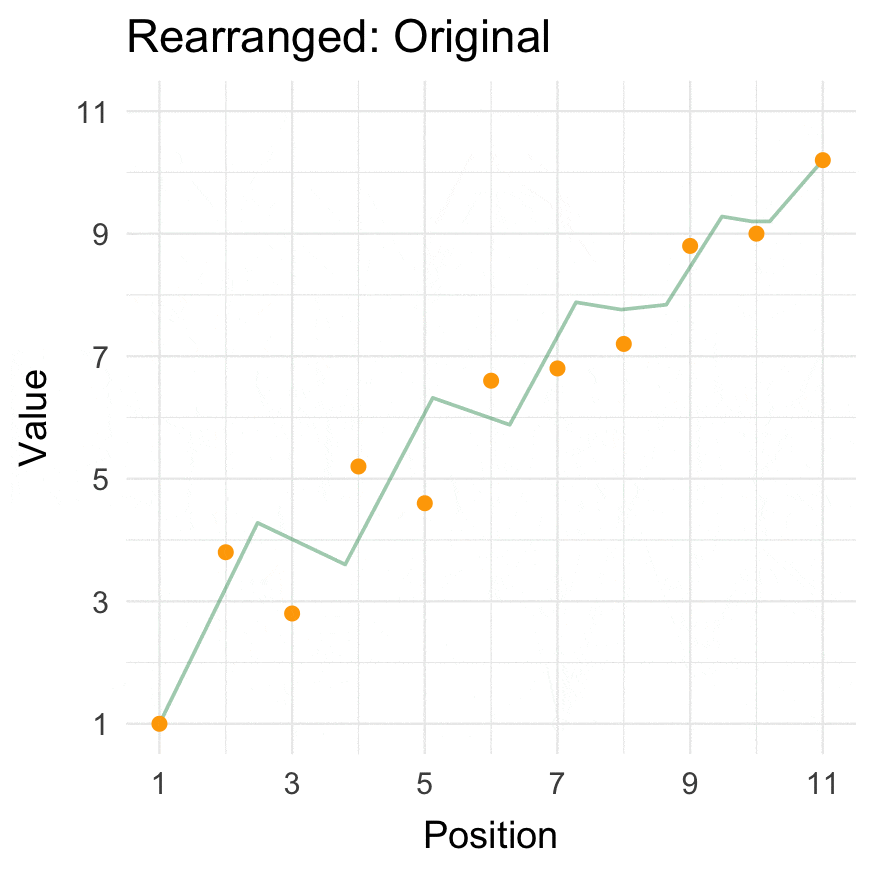
position_max() |
Position the highest value with values decreasing around it. |
position_min() |
Position the lowest value with values increasing around it. |
pair_extremes() |
Arrange as lowest, highest, 2nd lowest, 2nd highest, etc. |
triplet_extremes() |
Arrange as lowest, most middle, highest, 2nd lowest, 2nd most middle, 2nd highest, etc. |
closest_to() |
Order values by shortest distance to an origin. |
furthest_from() |
Order values by longest distance to an origin. |
rev_windows() |
Reverse order window-wise. |
roll_elements() |
Rolls/shifts positions of elements. |
shuffle_hierarchy() |
Shuffle multi-column hierarchy of groups. |
| Function | Description | Dimensions |
|---|---|---|
rotate_2d(),
rotate_3d() |
Rotate values around an origin in 2 or 3 dimensions. | 2 or 3 |
swirl_2d(),
swirl_3d() |
Swirl values around an origin in 2 or 3 dimensions. | 2 or 3 |
shear_2d(),
shear_3d() |
Shear values around an origin in 2 or 3 dimensions. | 2 or 3 |
expand_distances() |
Expand distances to an origin. | n |
expand_distances_each() |
Expand distances to an origin separately for each dimension. | n |
cluster_groups() |
Move data points into clusters around group centroids. | n |
dim_values() |
Dim values of a dimension by the distance to an n-dimensional origin. | n (alters 1) |
flip_values() |
Flip the values around an origin. | n |
roll_values() |
Shifts values and wraps to a range. | n |
wrap_to_range() |
Wraps values to a range. | n |
transfer_centroids() |
Transfer centroids from one
data.frame to another. |
n |
apply_transformation_matrix() |
Apply transformation matrix
to data.frame columns. |
n |
| Function | Description |
|---|---|
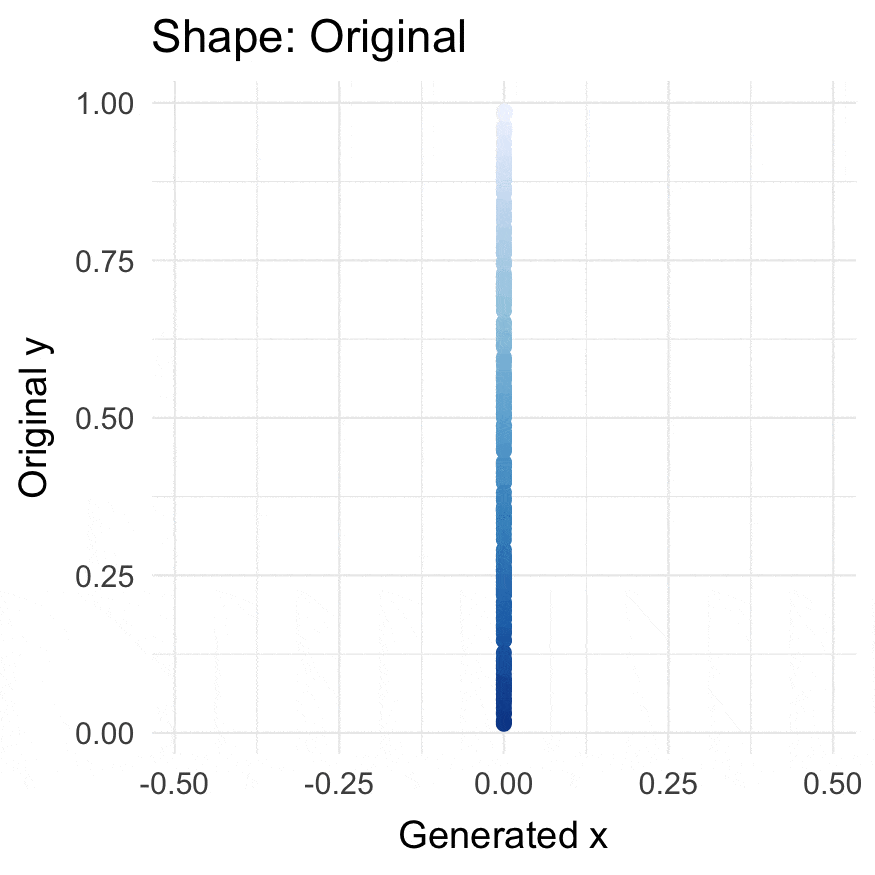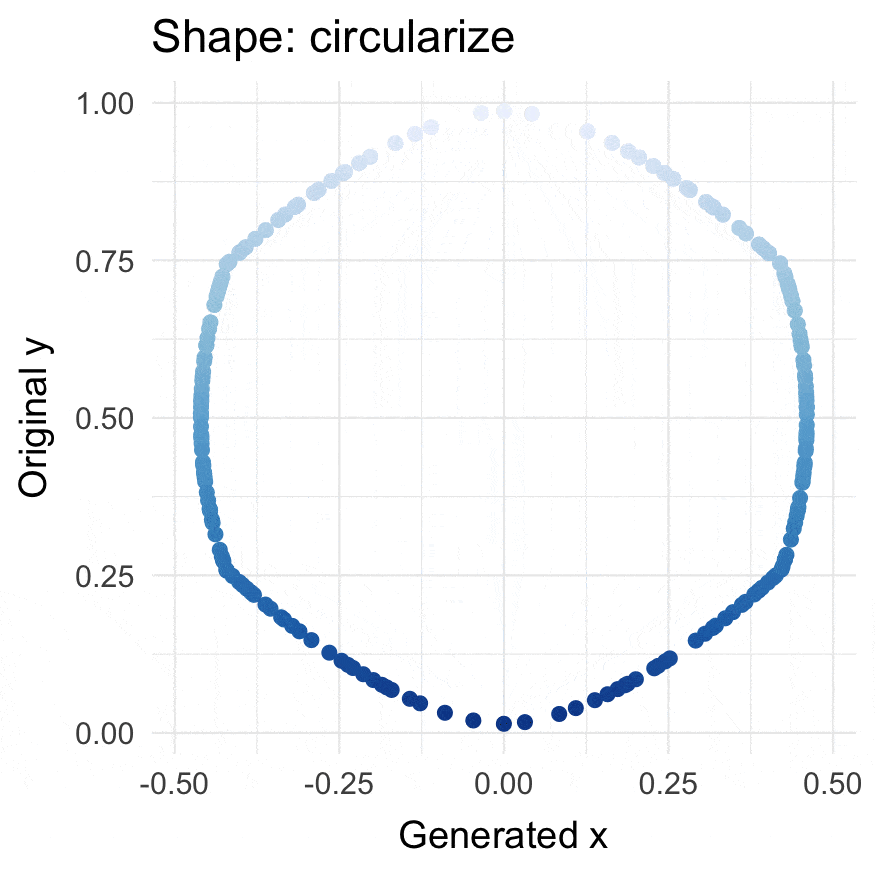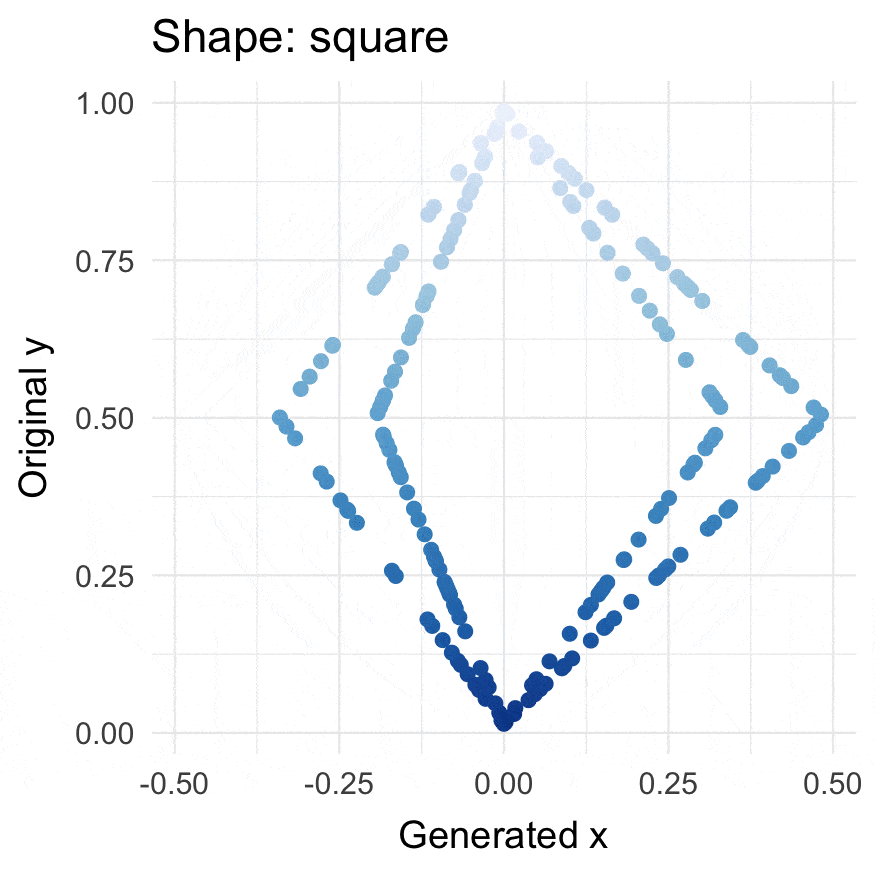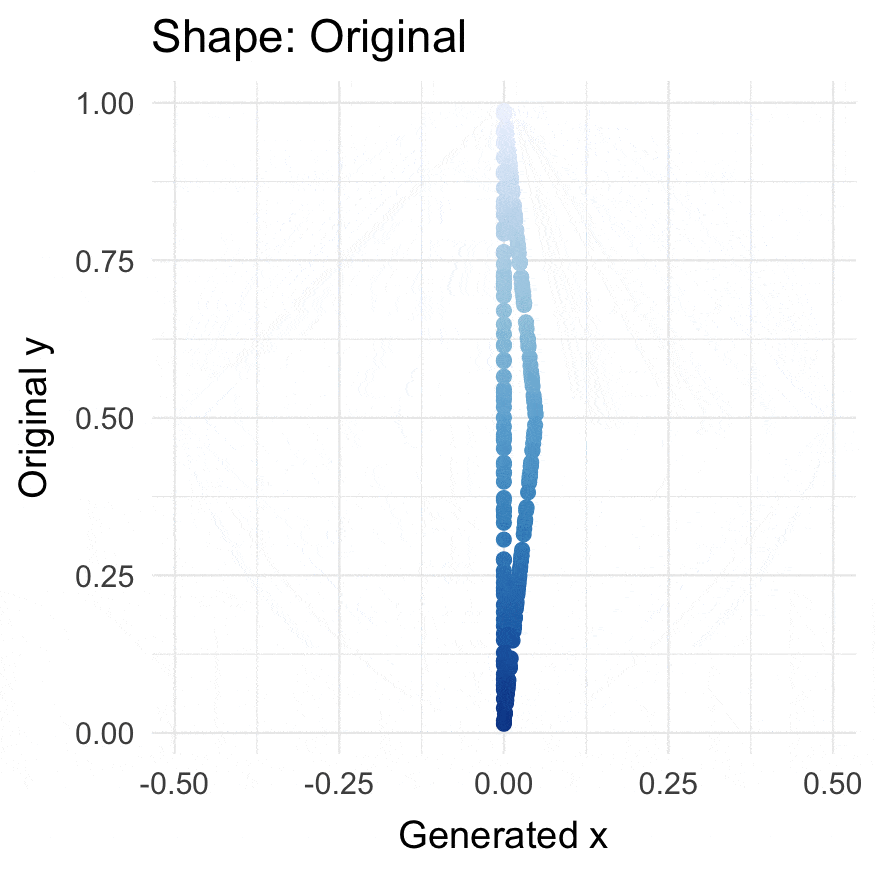
circularize() |
Create x-coordinates for y-coordinates so they form a circle. |
hexagonalize() |
Create x-coordinates for y-coordinates so they form a hexagon. |
square() |
Create x-coordinates for y-coordinates so they form a square. |
triangularize() |
Create x-coordinates for y-coordinates so they form a triangle. |
| Class | Description |
|---|---|
Pipeline |
Chain multiple transformations. |
GeneratedPipeline |
Chain multiple transformations and generate argument values per group. |
FixedGroupsPipeline |
Chain multiple transformations with different argument values per group. |
| Function | Description |
|---|---|
generate_clusters() |
Generate n-dimensional clusters. |
Additionally, some functions have *_vec() versions, that
take and return a vector.
Note: The available utility functions (like scalers, converters and measuring functions) are listed at the bottom of the readme.
Let’s see some examples. We start by attaching the necessary packages:
library(rearrr)
library(dplyr)
xpectr::set_test_seed(1)While we can use the functions with data.frames, we
showcase many of them with a vector for simplicity. At
times, we use the *_vec() version of a function in order to
get the output as a vector instead of a
data.frame.
The functions work with grouped data.frames and in
magrittr pipelines (%>%).
Rearrangers change the order of the data points.
center_max(data = 1:10)
#> [1] 1 3 5 7 9 10 8 6 4 2center_min(data = 1:10)
#> [1] 10 8 6 4 2 1 3 5 7 9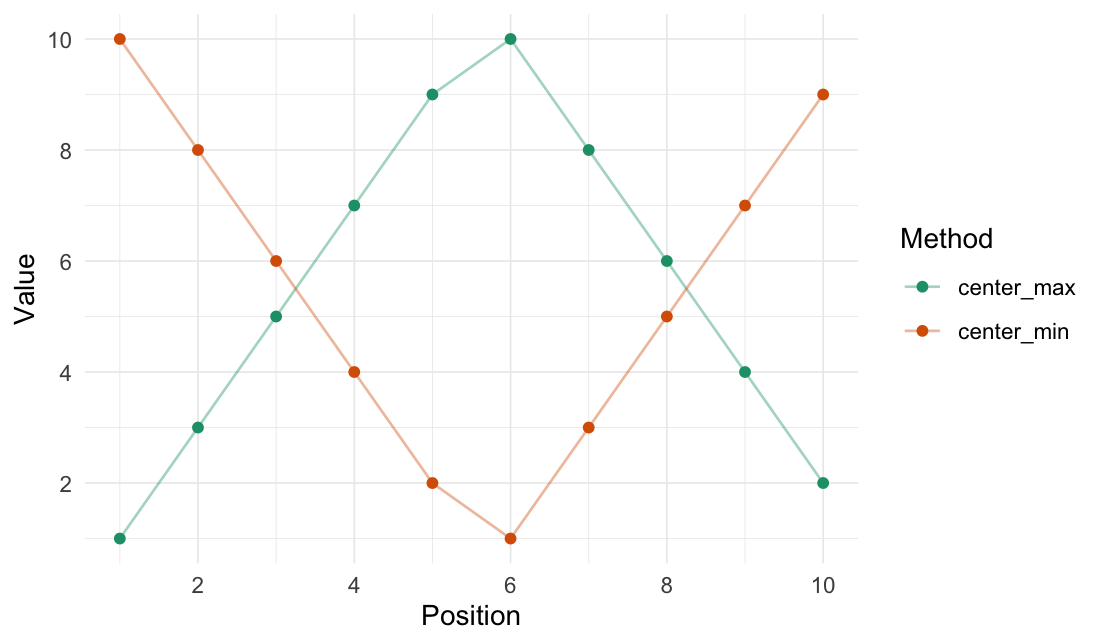
position_max(data = 1:10, position = 3)
#> [1] 6 8 10 9 7 5 4 3 2 1position_min(data = 1:10, position = 3)
#> [1] 5 3 1 2 4 6 7 8 9 10
pair_extremes(data = 1:10)
#> # A tibble: 10 × 2
#> Value .pair
#> <int> <fct>
#> 1 1 1
#> 2 10 1
#> 3 2 2
#> 4 9 2
#> 5 3 3
#> 6 8 3
#> 7 4 4
#> 8 7 4
#> 9 5 5
#> 10 6 5
We use the _vec() versions to get the reordered vectors.
For data.frames, use
closest_to()/furthest_from() instead.
The origin can be passed as either a specific coordinate (here, a
value in data) or a function.
closest_to_vec(data = 1:10, origin_fn = create_origin_fn(median))
#> [1] 5 6 4 7 3 8 2 9 1 10furthest_from_vec(data = 1:10, origin = 5)
#> [1] 10 1 9 2 8 3 7 4 6 5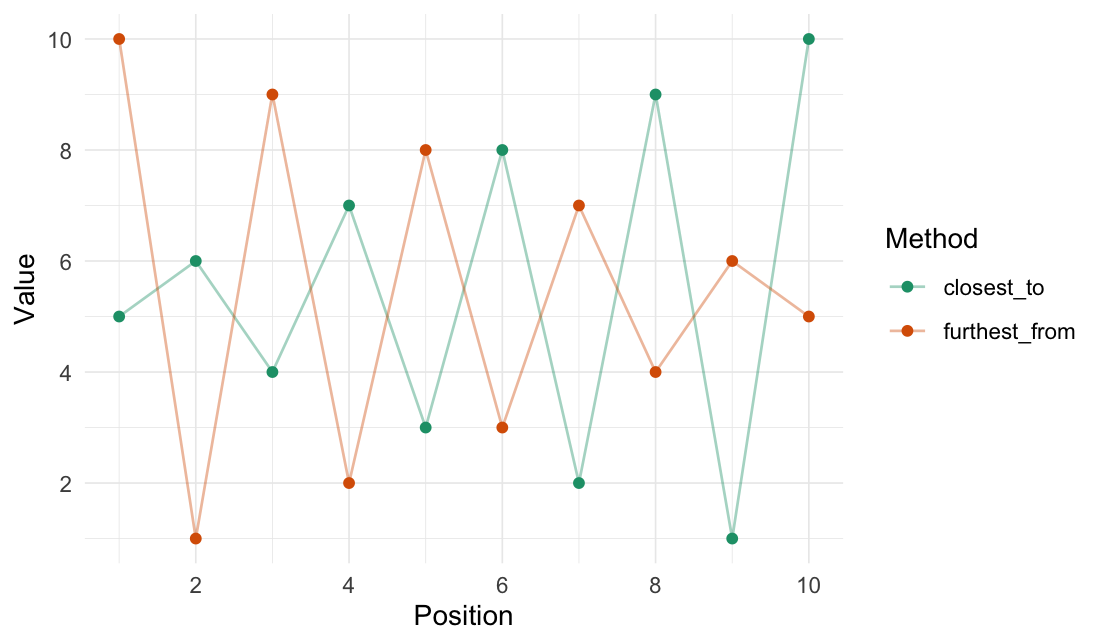
We use the _vec() version to get the reordered vector.
For data.frames, use rev_windows()
instead.
rev_windows_vec(data = 1:10, window_size = 3)
#> [1] 3 2 1 6 5 4 9 8 7 10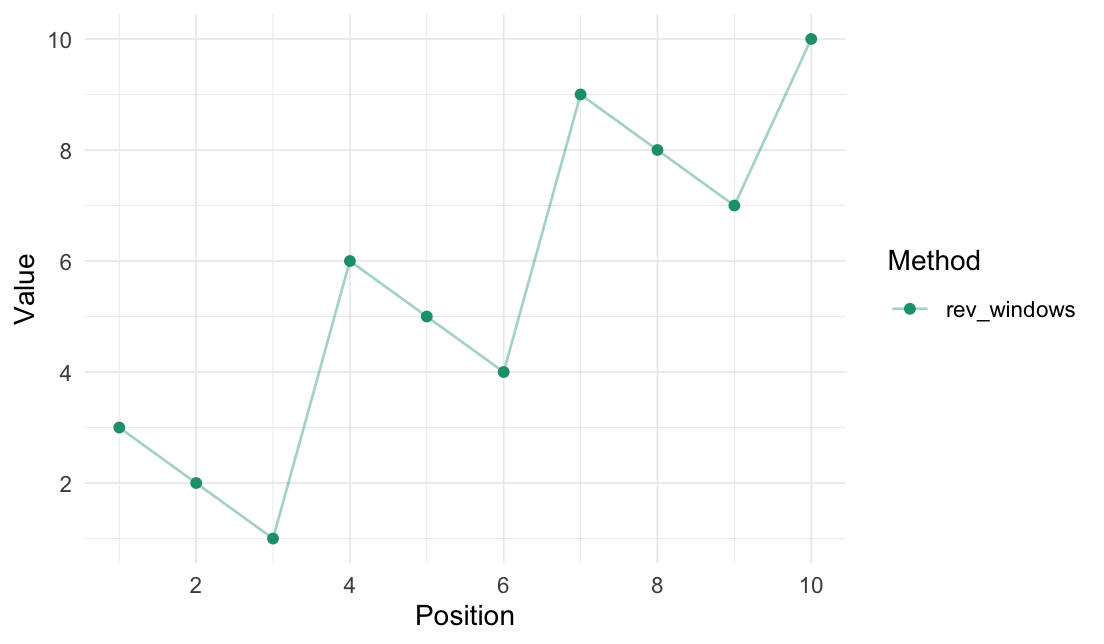
When having a data.frame with multiple grouping columns,
we can shuffle them one column (hierarchical level) at a time:
# Shuffle a given data frame 'df'
shuffle_hierarchy(df, group_cols = c("a", "b", "c"))The columns are shuffled one at a time, as so:
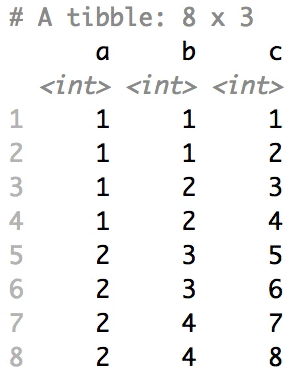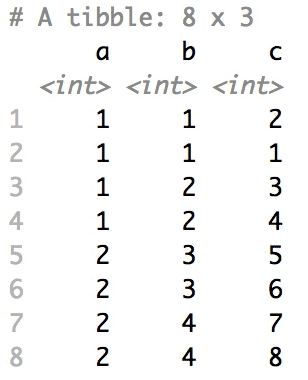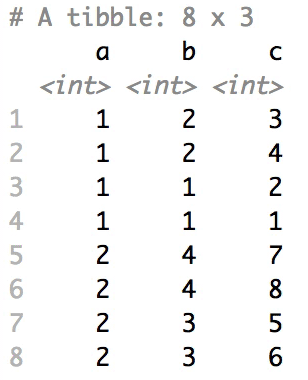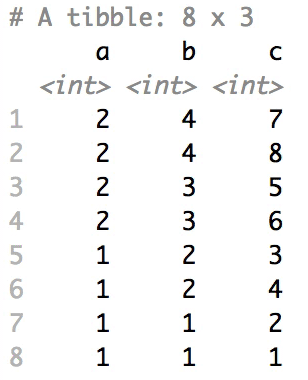
Mutators change the values of the data points.
2-dimensional rotation:
# Set seed for reproducibility
xpectr::set_test_seed(1)
# Draw random numbers
random_sample <- round(runif(10), digits = 4)
random_sample
#> [1] 0.2655 0.3721 0.5729 0.9082 0.2017 0.8984 0.9447 0.6608 0.6291 0.0618
rotate_2d(
data = random_sample,
degrees = 60,
origin_fn = centroid
)
#> # A tibble: 10 × 6
#> Index Value Index_rotated Value_rotated .origin .degrees
#> <int> <dbl> <dbl> <dbl> <list> <dbl>
#> 1 1 0.266 3.50 -3.49 <dbl [2]> 60
#> 2 2 0.372 3.91 -2.57 <dbl [2]> 60
#> 3 3 0.573 4.23 -1.60 <dbl [2]> 60
#> 4 4 0.908 4.44 -0.569 <dbl [2]> 60
#> 5 5 0.202 5.55 -0.0564 <dbl [2]> 60
#> 6 6 0.898 5.45 1.16 <dbl [2]> 60
#> 7 7 0.945 5.91 2.05 <dbl [2]> 60
#> 8 8 0.661 6.66 2.77 <dbl [2]> 60
#> 9 9 0.629 7.18 3.62 <dbl [2]> 60
#> 10 10 0.0618 8.17 4.20 <dbl [2]> 60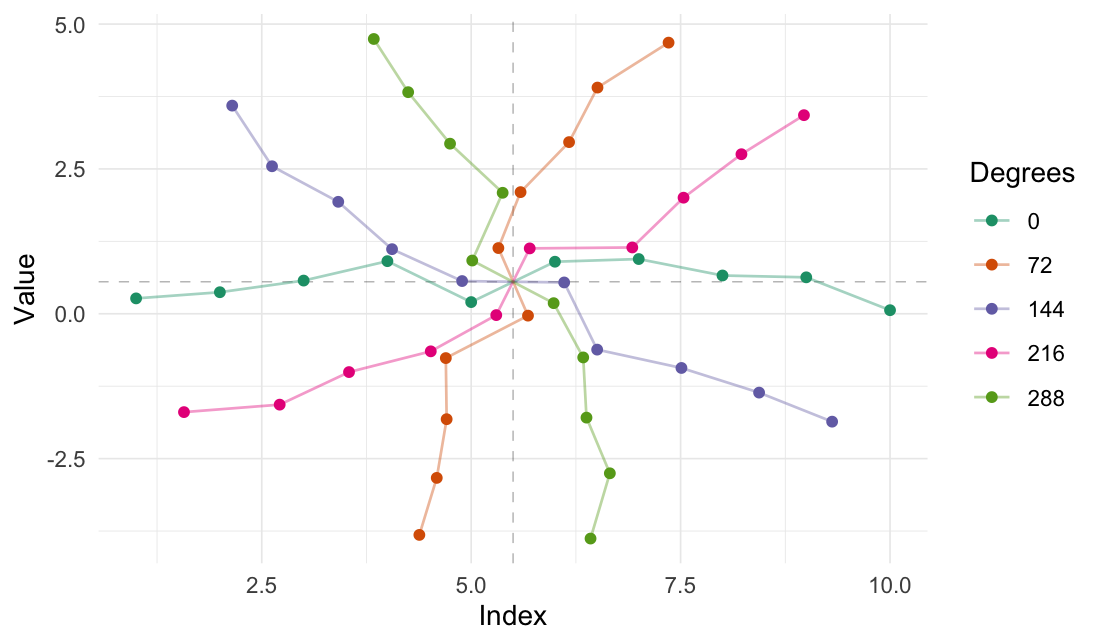
3-dimensional rotation:
# Set seed
set.seed(3)
# Create a data frame
df <- data.frame(
"x" = 1:12,
"y" = c(1, 2, 3, 4, 9, 10, 11,
12, 15, 16, 17, 18),
"z" = runif(12)
)
# Perform rotation
rotate_3d(
data = df,
x_col = "x",
y_col = "y",
z_col = "z",
x_deg = 45,
y_deg = 90,
z_deg = 135,
origin_fn = centroid
)
#> # A tibble: 12 × 9
#> x y z x_rotated y_rotated z_rotated .origin .degrees .degree…¹
#> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <list> <chr>
#> 1 1 1 0.168 15.3 9.54 5.96 <dbl [3]> <dbl [3]> x=45,y=9…
#> 2 2 2 0.808 14.3 10.2 4.96 <dbl [3]> <dbl [3]> x=45,y=9…
#> 3 3 3 0.385 13.3 9.76 3.96 <dbl [3]> <dbl [3]> x=45,y=9…
#> 4 4 4 0.328 12.3 9.70 2.96 <dbl [3]> <dbl [3]> x=45,y=9…
#> 5 5 9 0.602 7.33 9.97 1.96 <dbl [3]> <dbl [3]> x=45,y=9…
#> 6 6 10 0.604 6.33 9.98 0.962 <dbl [3]> <dbl [3]> x=45,y=9…
#> 7 7 11 0.125 5.33 9.50 -0.0384 <dbl [3]> <dbl [3]> x=45,y=9…
#> 8 8 12 0.295 4.33 9.67 -1.04 <dbl [3]> <dbl [3]> x=45,y=9…
#> 9 9 15 0.578 1.33 9.95 -2.04 <dbl [3]> <dbl [3]> x=45,y=9…
#> 10 10 16 0.631 0.333 10.0 -3.04 <dbl [3]> <dbl [3]> x=45,y=9…
#> 11 11 17 0.512 -0.667 9.88 -4.04 <dbl [3]> <dbl [3]> x=45,y=9…
#> 12 12 18 0.505 -1.67 9.88 -5.04 <dbl [3]> <dbl [3]> x=45,y=9…
#> # … with abbreviated variable name ¹.degrees_str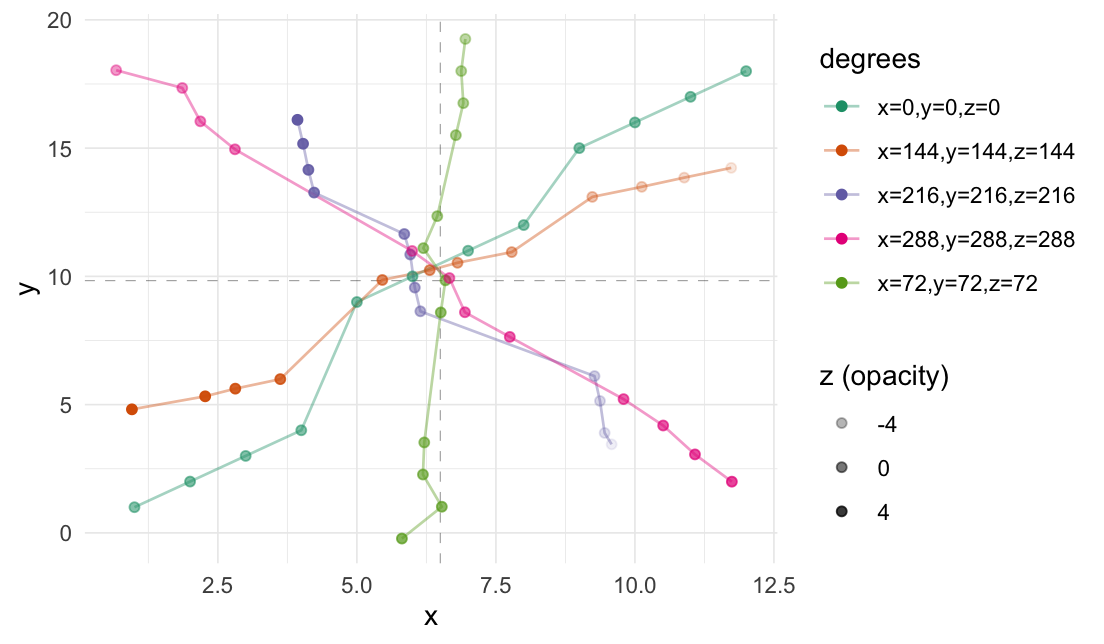
2-dimensional swirling:
# Rotate values
swirl_2d(data = rep(1, 50), radius = 95, origin = c(0, 0))
#> # A tibble: 50 × 7
#> Index Value Index_swirled Value_swirled .origin .degrees .radius
#> <int> <dbl> <dbl> <dbl> <list> <dbl> <dbl>
#> 1 1 1 0.952 1.05 <dbl [2]> 2.68 95
#> 2 2 1 1.92 1.15 <dbl [2]> 4.24 95
#> 3 3 1 2.88 1.31 <dbl [2]> 5.99 95
#> 4 4 1 3.83 1.53 <dbl [2]> 7.81 95
#> 5 5 1 4.76 1.82 <dbl [2]> 9.66 95
#> 6 6 1 5.68 2.18 <dbl [2]> 11.5 95
#> 7 7 1 6.58 2.59 <dbl [2]> 13.4 95
#> 8 8 1 7.45 3.07 <dbl [2]> 15.3 95
#> 9 9 1 8.30 3.61 <dbl [2]> 17.2 95
#> 10 10 1 9.13 4.21 <dbl [2]> 19.0 95
#> # … with 40 more rows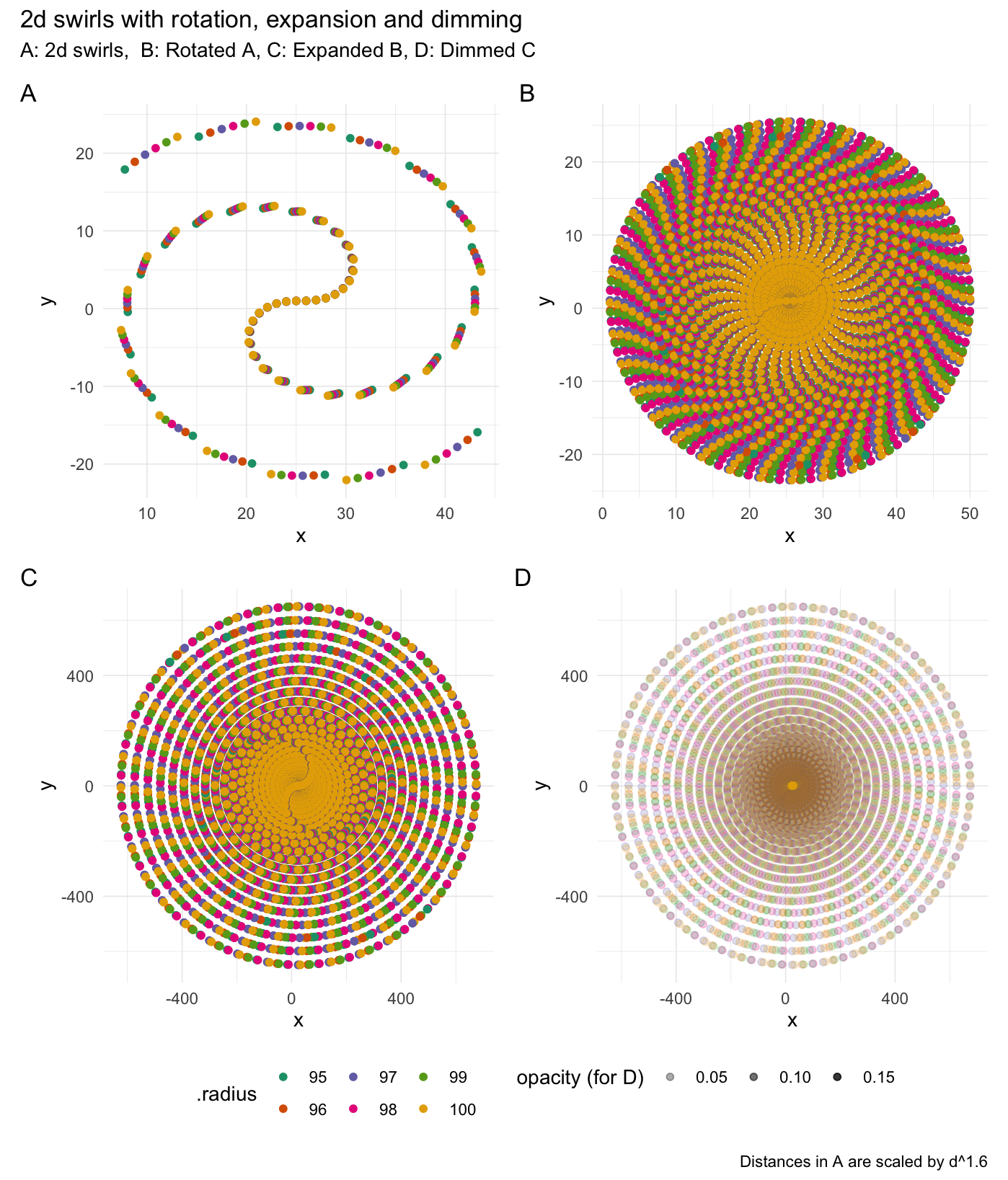
3-dimensional swirling:
# Set seed
set.seed(4)
# Create a data frame
df <- data.frame(
"x" = 1:50,
"y" = 1:50,
"z" = 1:50,
"r1" = runif(50),
"r2" = runif(50) * 35,
"o" = 1,
"g" = rep(1:5, each = 10)
)
# They see me swiiirling
swirl_3d(
data = df,
x_radius = 45,
x_col = "x",
y_col = "y",
z_col = "z",
origin = c(0, 0, 0),
keep_original = FALSE
)
#> # A tibble: 50 × 7
#> x_swirled y_swirled z_swirled .origin .degrees .radius .radius_str
#> <dbl> <dbl> <dbl> <list> <list> <list> <chr>
#> 1 1 0.872 1.11 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 2 2 1.46 2.42 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 3 3 1.74 3.87 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 4 4 1.68 5.40 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 5 5 1.27 6.96 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 6 6 0.508 8.47 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 7 7 -0.604 9.88 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 8 8 -2.05 11.1 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 9 9 -3.80 12.1 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> 10 10 -5.82 12.9 <dbl [3]> <dbl [3]> <dbl [3]> x=45,y=0,z=0
#> # … with 40 more rows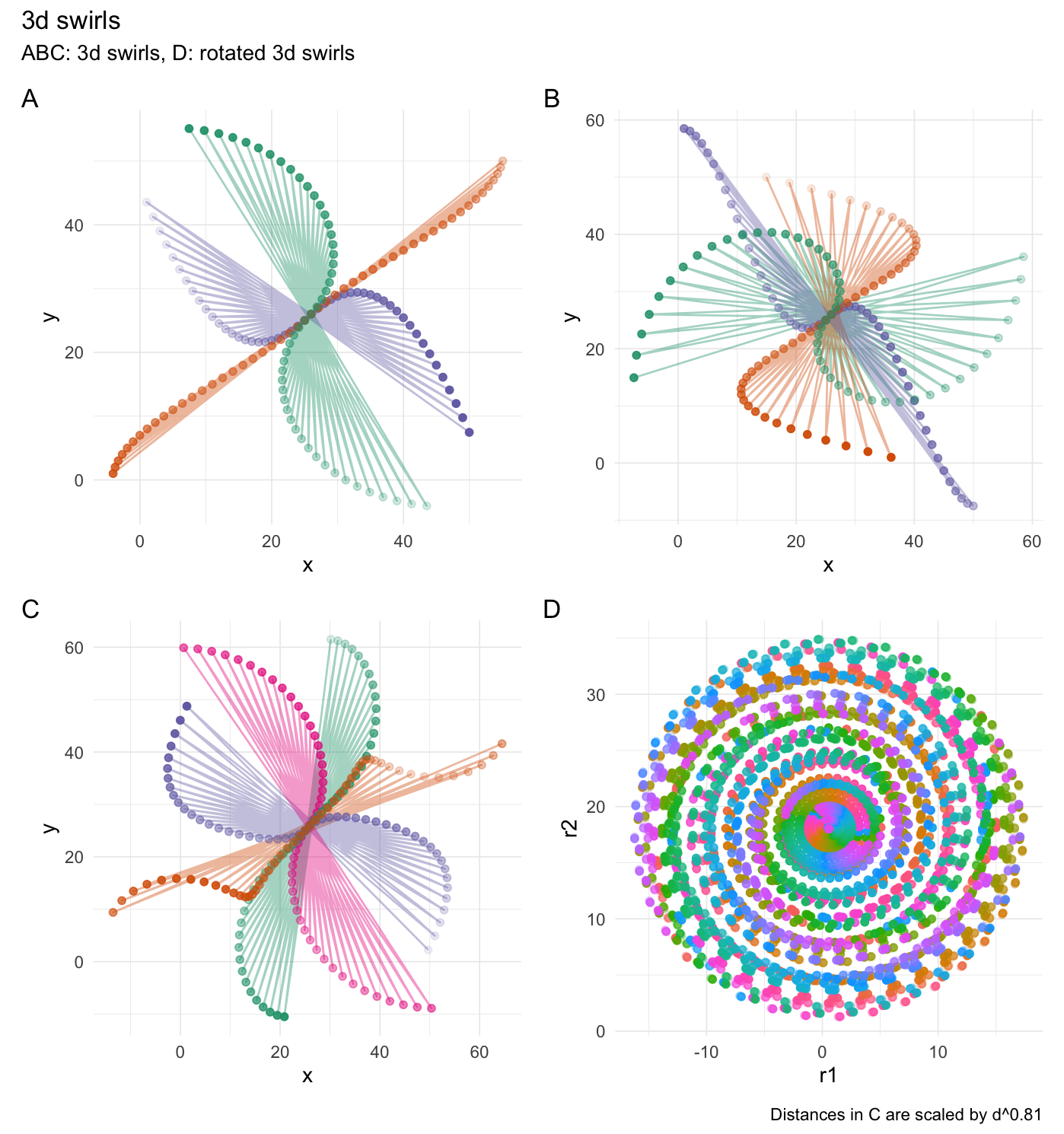
# 1d expansion
expand_distances(
data = random_sample,
multiplier = 3,
origin_fn = centroid,
exponentiate = TRUE
)
#> # A tibble: 10 × 4
#> Value Value_expanded .exponent .origin
#> <dbl> <dbl> <dbl> <list>
#> 1 0.266 -0.575 3 <dbl [1]>
#> 2 0.372 -0.0891 3 <dbl [1]>
#> 3 0.573 0.617 3 <dbl [1]>
#> 4 0.908 2.05 3 <dbl [1]>
#> 5 0.202 -0.908 3 <dbl [1]>
#> 6 0.898 1.99 3 <dbl [1]>
#> 7 0.945 2.26 3 <dbl [1]>
#> 8 0.661 0.916 3 <dbl [1]>
#> 9 0.629 0.803 3 <dbl [1]>
#> 10 0.0618 -1.75 3 <dbl [1]>2d expansion:

Expand differently in each axis:
# Expand x-axis and contract y-axis
expand_distances_each(
data.frame("x" = runif(10),
"y" = runif(10)),
cols = c("x", "y"),
multipliers = c(7, 0.5),
origin_fn = centroid
)
#> # A tibble: 10 × 7
#> x y x_expanded y_expanded .multipliers .multipliers_str .origin
#> <dbl> <dbl> <dbl> <dbl> <list> <chr> <list>
#> 1 0.622 0.284 1.37 0.309 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 2 0.675 0.610 1.74 0.472 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 3 0.802 0.524 2.63 0.428 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 4 0.260 0.0517 -1.17 0.192 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 5 0.760 0.0757 2.33 0.204 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 6 0.0199 0.414 -2.85 0.373 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 7 0.955 0.578 3.70 0.455 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 8 0.437 0.110 0.0675 0.222 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 9 0.0892 0.511 -2.36 0.422 <dbl [2]> x=7,y=0.5 <dbl [2]>
#> 10 0.361 0.169 -0.466 0.251 <dbl [2]> x=7,y=0.5 <dbl [2]>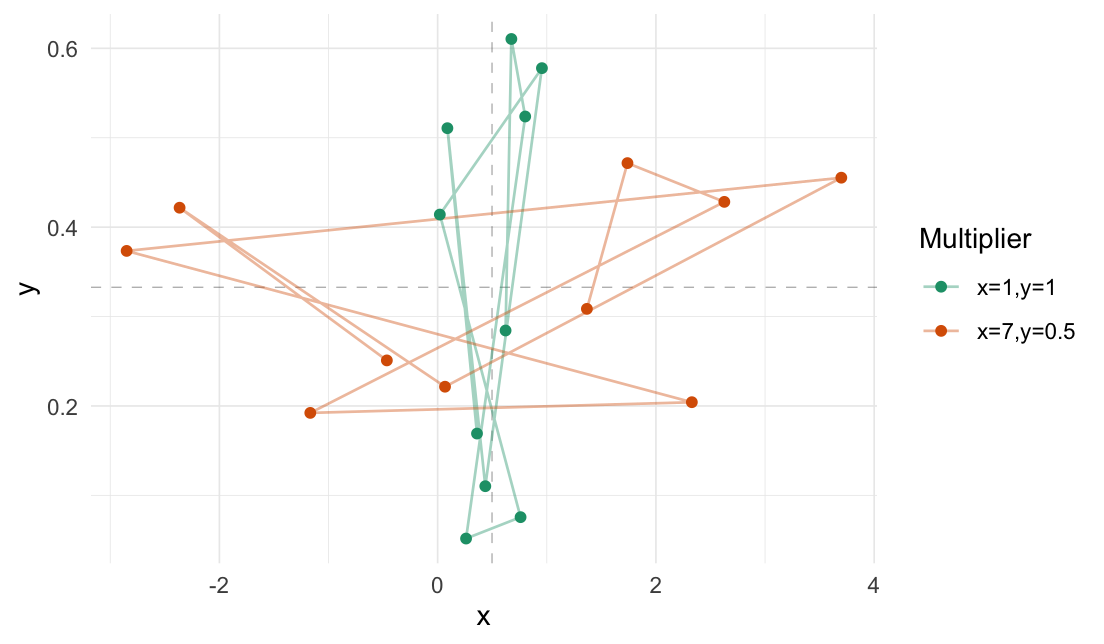
# Set seed for reproducibility
xpectr::set_test_seed(3)
# Create data frame with random data and a grouping variable
df <- data.frame(
"x" = runif(50),
"y" = runif(50),
"g" = rep(c(1, 2, 3, 4, 5), each = 10)
)
cluster_groups(
data = df,
cols = c("x", "y"),
group_col = "g"
)
#> # A tibble: 50 × 5
#> x y x_clustered y_clustered g
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0.168 0.229 0.335 0.420 1
#> 2 0.808 0.213 0.449 0.417 1
#> 3 0.385 0.877 0.374 0.540 1
#> 4 0.328 0.993 0.364 0.562 1
#> 5 0.602 0.844 0.413 0.534 1
#> 6 0.604 0.910 0.413 0.547 1
#> 7 0.125 0.471 0.328 0.465 1
#> 8 0.295 0.224 0.358 0.419 1
#> 9 0.578 0.128 0.408 0.401 1
#> 10 0.631 0.280 0.418 0.429 1
#> # … with 40 more rows
# Add a column with 1s
df_clustered$o <- 1
# Dim the "o" column based on the data point's distance
# to the most central point in the cluster
df_clustered %>%
dplyr::group_by(g) %>%
dim_values(
cols = c("x_clustered", "y_clustered"),
dim_col = "o",
origin_fn = most_centered
)
#> # A tibble: 50 × 6
#> x_clustered y_clustered g o o_dimmed .origin
#> <dbl> <dbl> <dbl> <dbl> <dbl> <list>
#> 1 0.335 0.420 1 1 0.853 <dbl [2]>
#> 2 0.449 0.417 1 1 0.936 <dbl [2]>
#> 3 0.374 0.540 1 1 0.798 <dbl [2]>
#> 4 0.364 0.562 1 1 0.765 <dbl [2]>
#> 5 0.413 0.534 1 1 0.819 <dbl [2]>
#> 6 0.413 0.547 1 1 0.801 <dbl [2]>
#> 7 0.328 0.465 1 1 0.831 <dbl [2]>
#> 8 0.358 0.419 1 1 0.889 <dbl [2]>
#> 9 0.408 0.401 1 1 0.943 <dbl [2]>
#> 10 0.418 0.429 1 1 1 <dbl [2]>
#> # … with 40 more rows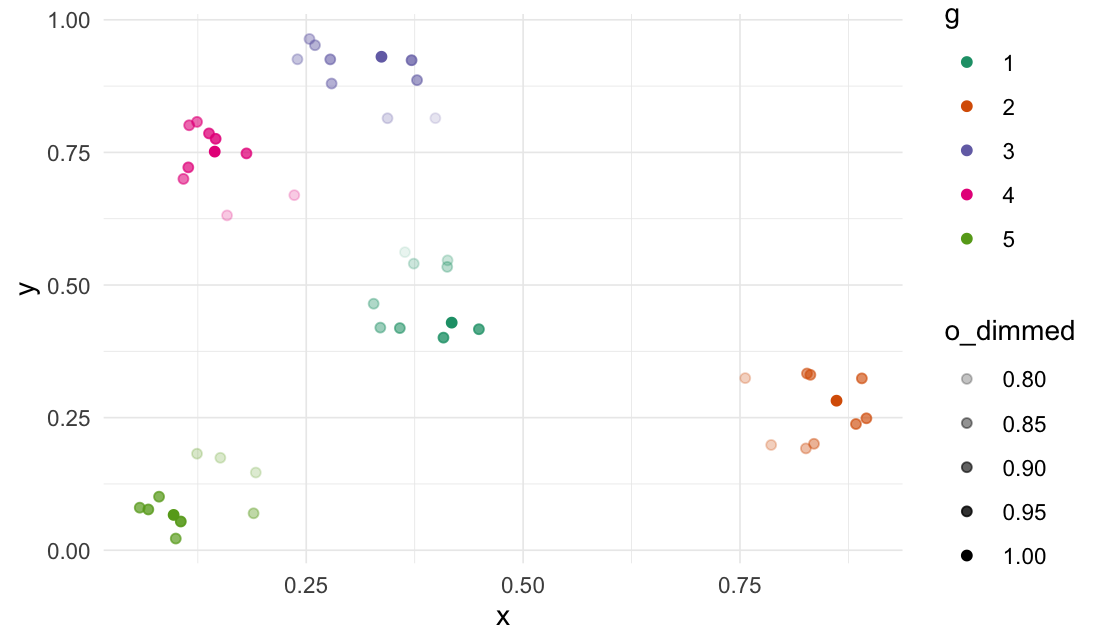
# The median value to flip around
median(random_sample)
#> [1] 0.601
# Flip the random numbers around the median
flip_values(
data = random_sample,
origin_fn = create_origin_fn(median)
)
#> # A tibble: 10 × 3
#> Value Value_flipped .origin
#> <dbl> <dbl> <list>
#> 1 0.266 0.936 <dbl [1]>
#> 2 0.372 0.830 <dbl [1]>
#> 3 0.573 0.629 <dbl [1]>
#> 4 0.908 0.294 <dbl [1]>
#> 5 0.202 1.00 <dbl [1]>
#> 6 0.898 0.304 <dbl [1]>
#> 7 0.945 0.257 <dbl [1]>
#> 8 0.661 0.541 <dbl [1]>
#> 9 0.629 0.573 <dbl [1]>
#> 10 0.0618 1.14 <dbl [1]>
circularize(runif(200))
#> # A tibble: 200 × 4
#> Value .circle_x .degrees .origin
#> <dbl> <dbl> <dbl> <list>
#> 1 0.766 -0.418 148. <dbl [2]>
#> 2 0.682 0.461 21.3 <dbl [2]>
#> 3 0.209 -0.398 216. <dbl [2]>
#> 4 0.712 0.448 25.1 <dbl [2]>
#> 5 0.605 0.484 12.0 <dbl [2]>
#> 6 0.341 0.467 341. <dbl [2]>
#> 7 0.0412 -0.178 249. <dbl [2]>
#> 8 0.402 -0.484 192. <dbl [2]>
#> 9 0.0791 0.256 301. <dbl [2]>
#> 10 0.313 -0.457 203. <dbl [2]>
#> # … with 190 more rows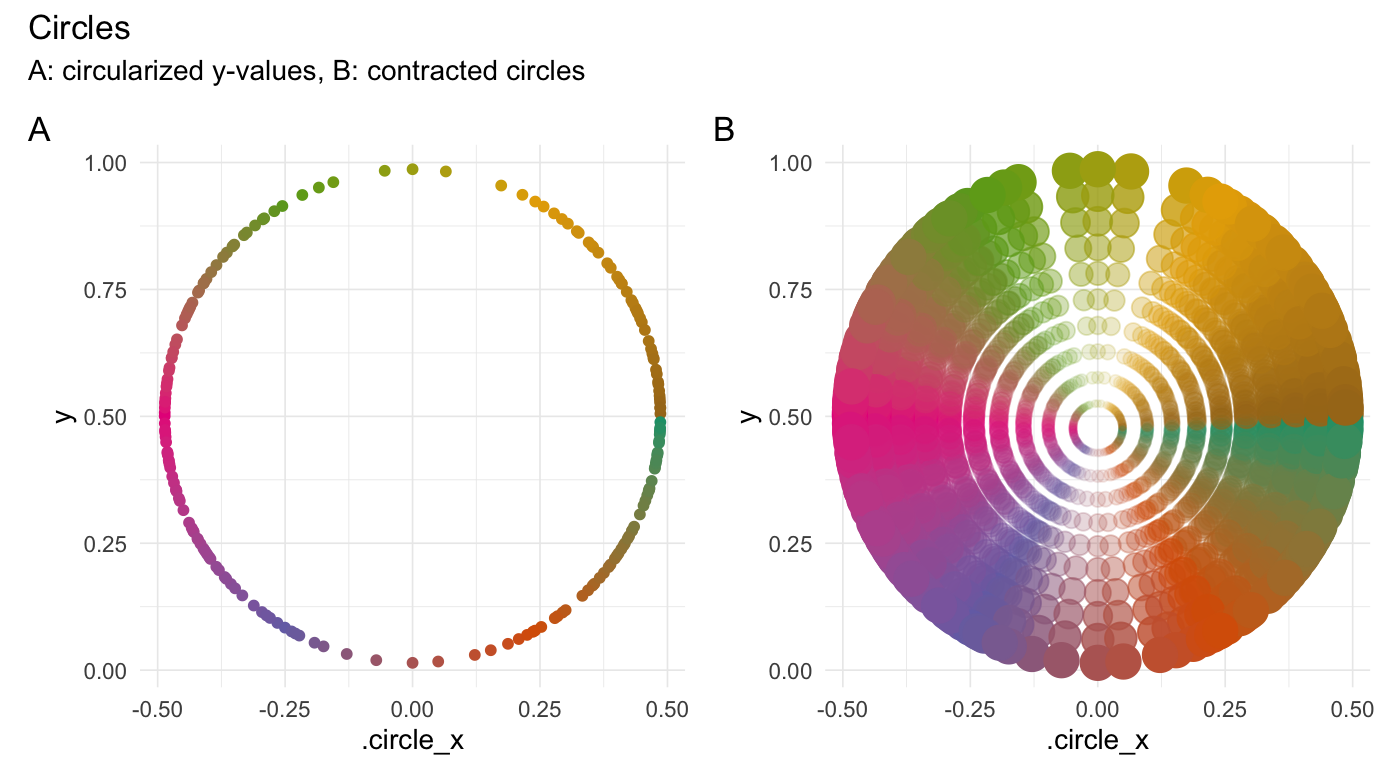
hexagonalize(runif(200))
#> # A tibble: 200 × 3
#> Value .hexagon_x .edge
#> <dbl> <dbl> <fct>
#> 1 0.0983 -0.0945 4
#> 2 0.319 -0.413 5
#> 3 0.996 0.00215 1
#> 4 0.726 -0.413 5
#> 5 0.687 -0.413 5
#> 6 0.629 -0.413 5
#> 7 0.803 0.335 1
#> 8 0.543 0.413 2
#> 9 0.862 0.234 1
#> 10 0.984 -0.0222 6
#> # … with 190 more rows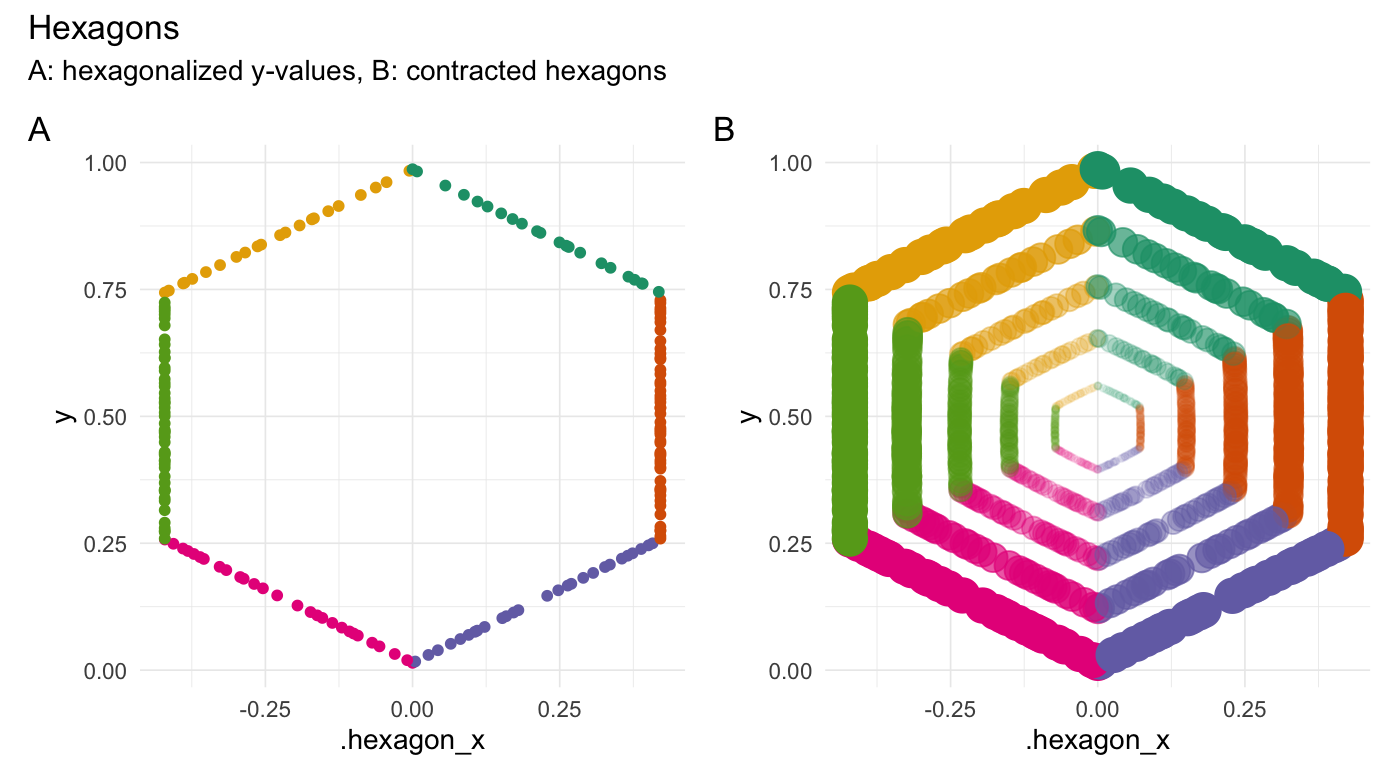
square(runif(200))
#> # A tibble: 200 × 3
#> Value .square_x .edge
#> <dbl> <dbl> <fct>
#> 1 0.296 0.291 2
#> 2 0.231 0.225 2
#> 3 0.914 0.0854 1
#> 4 0.332 0.327 2
#> 5 0.556 -0.443 4
#> 6 0.582 -0.418 4
#> 7 0.217 0.212 2
#> 8 0.205 0.200 2
#> 9 0.970 0.0297 1
#> 10 0.801 -0.199 4
#> # … with 190 more rows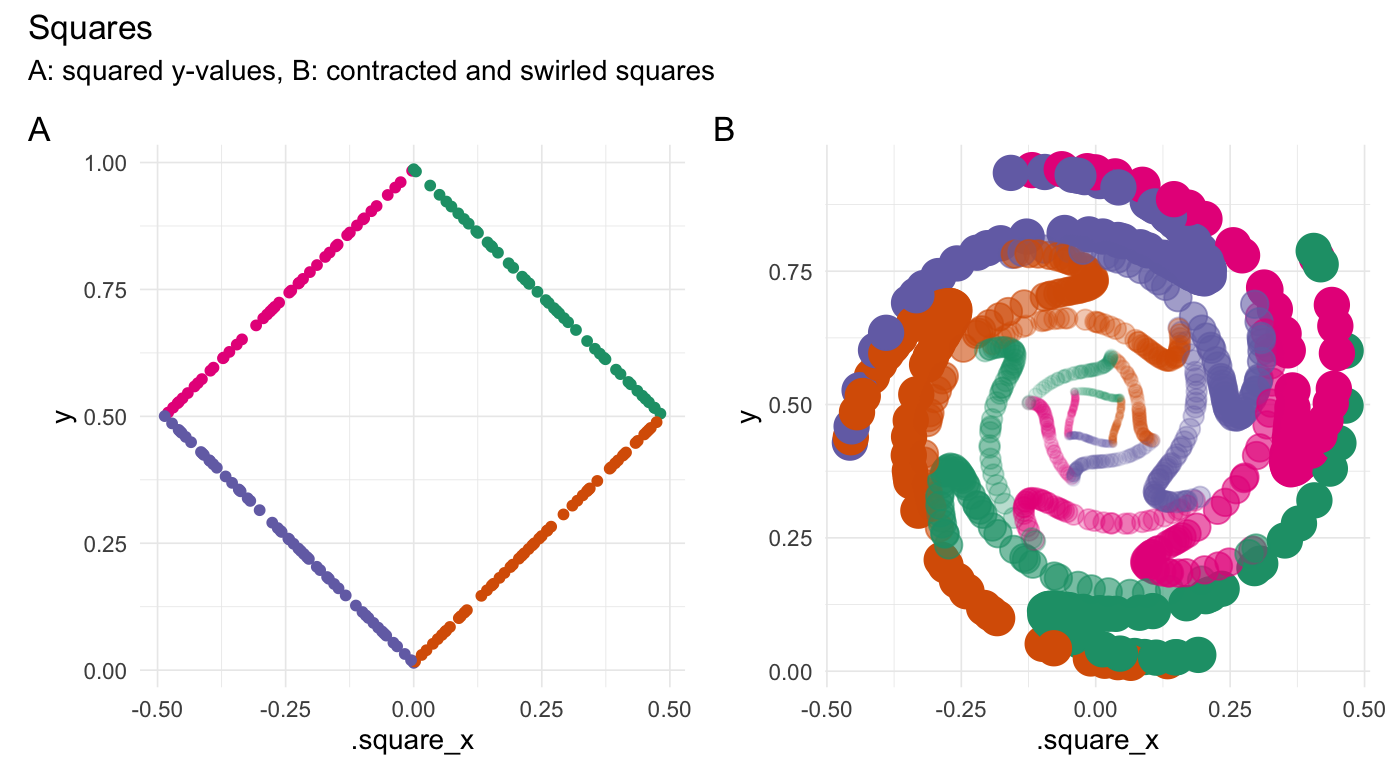
triangularize(runif(200))
#> # A tibble: 200 × 3
#> Value .triangle_x .edge
#> <dbl> <dbl> <fct>
#> 1 0.00823 0 3
#> 2 0.986 0 3
#> 3 0.519 0.473 1
#> 4 0.662 0 3
#> 5 0.632 0.360 1
#> 6 0.734 0.258 1
#> 7 0.668 0 3
#> 8 0.642 0.350 1
#> 9 0.584 0.409 1
#> 10 0.741 0 3
#> # … with 190 more rows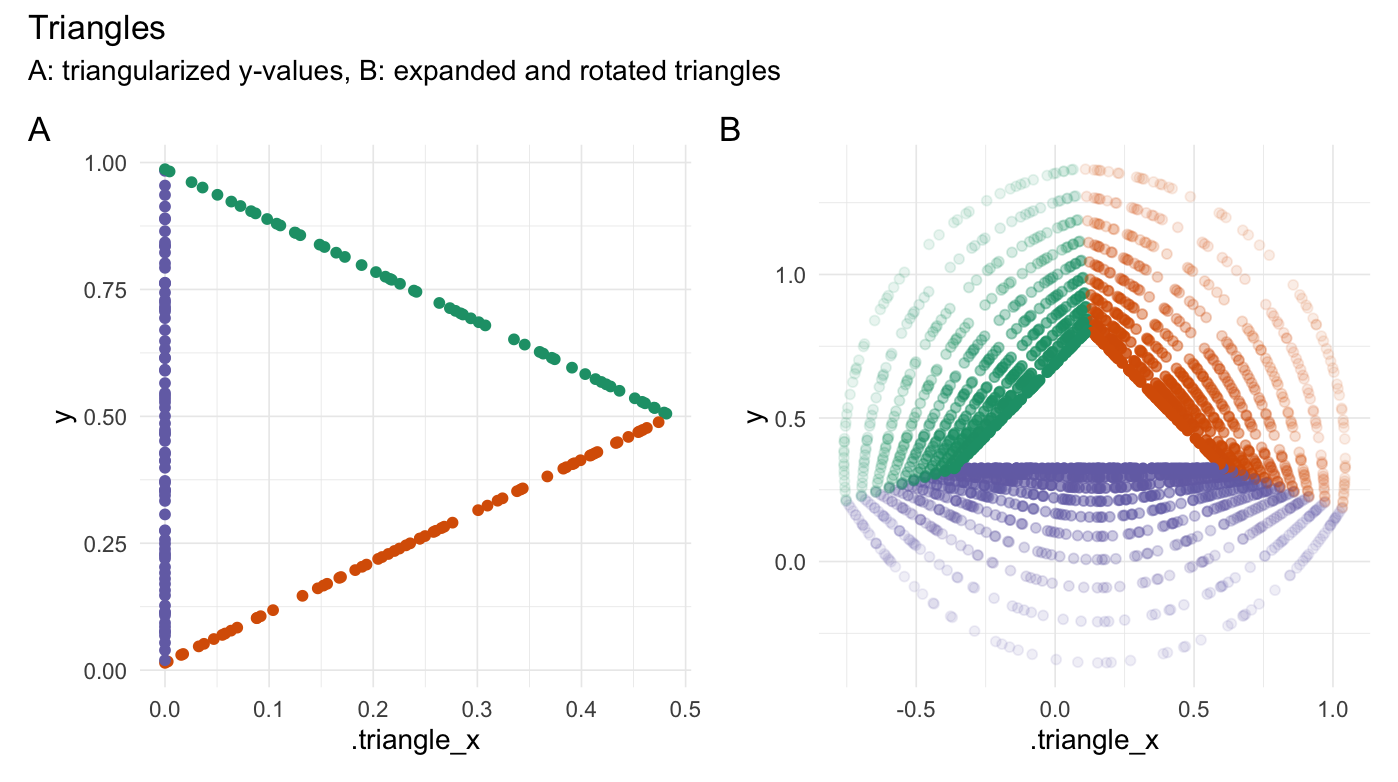
generate_clusters(
num_rows = 50,
num_cols = 5,
num_clusters = 5,
compactness = 1.6
)
#> # A tibble: 50 × 6
#> D1 D2 D3 D4 D5 .cluster
#> <dbl> <dbl> <dbl> <dbl> <dbl> <fct>
#> 1 0.316 0.553 0.523 0.202 0.653 1
#> 2 0.279 0.753 0.447 0.0774 0.788 1
#> 3 0.301 0.516 0.530 0.0541 0.842 1
#> 4 0.350 0.594 0.540 0.0701 0.922 1
#> 5 0.239 0.497 0.677 0.102 0.621 1
#> 6 0.264 0.632 0.670 0.0742 0.845 1
#> 7 0.273 0.589 0.696 0.0681 0.885 1
#> 8 0.273 0.592 0.559 0.0944 0.987 1
#> 9 0.336 0.569 0.618 0.212 0.670 1
#> 10 0.302 0.605 0.545 0.0601 0.938 1
#> # … with 40 more rows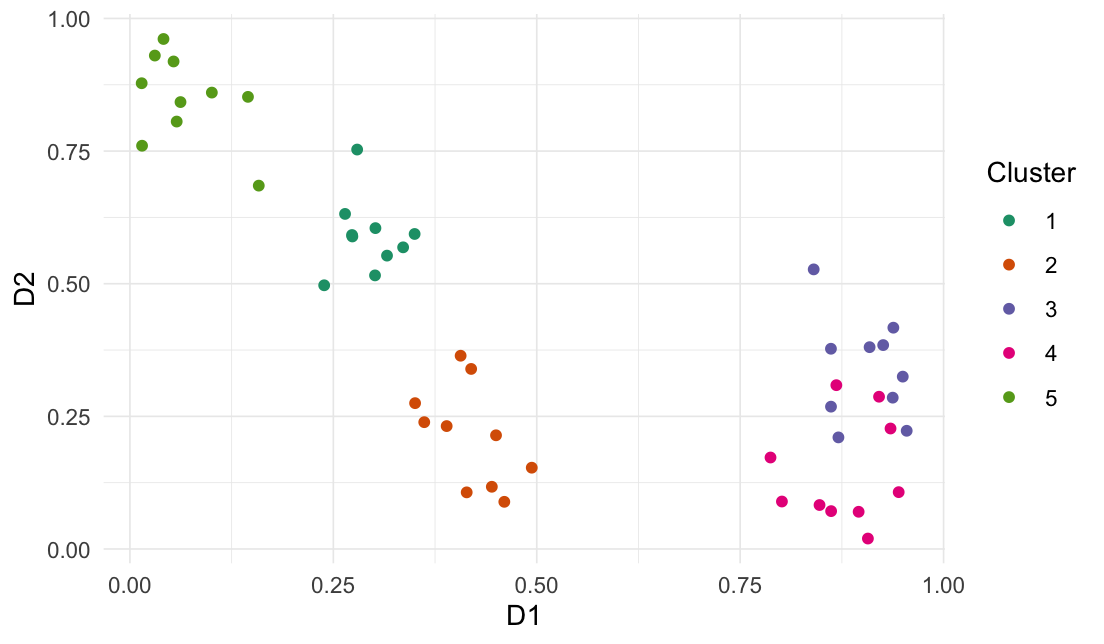
| Function | Description |
|---|---|
radians_to_degrees() |
Converts radians to degrees. |
degrees_to_radians() |
Converts degrees to radians. |
| Function | Description |
|---|---|
min_max_scale() |
Scale values to a range. |
to_unit_length() |
Scale vectors to unit length row-wise or column-wise. |
| Function | Description |
|---|---|
distance() |
Calculates distance to an origin. |
angle() |
Calculates angle between points and an origin. |
vector_length() |
Calculates vector length/magnitude row-wise or column-wise. |
| Function | Description |
|---|---|
create_origin_fn() |
Creates function for finding origin
coordinates (like centroid()). |
centroid() |
Calculates the mean of each supplied vector/column. |
most_centered() |
Finds coordinates of data point closest to the centroid. |
is_most_centered() |
Indicates whether a data point is the most centered. |
midrange() |
Calculates the midrange of each supplied vector/column. |
create_n_fn() |
Creates function for finding the number of positions to move. |
median_index() |
Calculates median index of each supplied vector. |
quantile_index() |
Calculates quantile of indices for each supplied vector. |