

A scalable method to estimates joint Species Distribution Models (jSDMs) based on the multivariate probit model through Monte-Carlo approximation of the joint likelihood. The numerical approximation is based on ‘PyTorch’ and ‘reticulate’, and can be calculated on CPUs and GPUs alike.
The method is described in Pichler & Hartig (2021) A new joint species distribution model for faster and more accurate inference of species associations from big community data.
The package includes options to fit various different (j)SDM models:
To get more information, install the package and run
library(sjSDM)
?sjSDM
vignette("sjSDM", package="sjSDM")sjSDM is based on ‘PyTorch’, a ‘python’ library, and thus requires ‘python’ dependencies. The ‘python’ dependencies can be automatically installed by running:
library(sjSDM)
install_sjSDM()If this didn’t work, please check the troubleshooting guide:
library(sjSDM)
?installation_helpLet’s first simulate a community data set:
library(sjSDM)
## ── Attaching sjSDM ──────────────────────────────────────────────────── 1.0.1 ──
## ✓ torch <environment>
## ✓ torch_optimizer
## ✓ pyro
## ✓ madgrad
set.seed(42)
community <- simulate_SDM(sites = 100, species = 10, env = 3, se = TRUE)
Env <- community$env_weights
Occ <- community$response
SP <- matrix(rnorm(200, 0, 0.3), 100, 2) # spatial coordinates (no effect on species occurences)Estimate jSDM:
model <- sjSDM(Y = Occ, env = linear(data = Env, formula = ~X1), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=binomial("probit"), sampling = 100L)
summary(model)
## LogLik: -569.5459
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.3380 1.0000
## sp3 -0.0310 -0.3640 1.0000
## sp4 0.0890 -0.2770 0.6670 1.0000
## sp5 0.4590 -0.3710 -0.0140 -0.0960 1.0000
## sp6 -0.1190 0.3690 0.1730 0.1980 -0.0770 1.0000
## sp7 0.4290 -0.1860 0.1700 0.1470 0.5150 0.2420 1.0000
## sp8 0.2490 0.0510 -0.3270 -0.3430 0.3090 -0.0230 0.2280 1.0000
## sp9 0.0450 -0.0290 0.0060 0.1660 -0.3590 -0.2000 -0.3070 -0.1840 1.0000
## sp10 0.2910 0.3150 -0.5000 -0.3540 0.1800 0.1080 0.1860 0.3410 -0.0710 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7
## X1:X2 0.1362036 -0.4616366 0.3906074 -0.1906729 0.4108464 0.1651098 0.4153814
## sp8 sp9 sp10
## X1:X2 0.2773075 0.2295802 -0.02492988
##
##
##
## Estimate Std.Err Z value Pr(>|z|)
## sp1 (Intercept) -0.0405 0.1998 -0.20 0.83921
## sp1 X1 0.6836 0.3973 1.72 0.08527 .
## sp2 (Intercept) -0.0101 0.2120 -0.05 0.96207
## sp2 X1 0.9244 0.4110 2.25 0.02450 *
## sp3 (Intercept) -0.2737 0.2150 -1.27 0.20302
## sp3 X1 0.9865 0.4143 2.38 0.01726 *
## sp4 (Intercept) -0.0560 0.2111 -0.27 0.79074
## sp4 X1 -1.1353 0.4182 -2.71 0.00663 **
## sp5 (Intercept) -0.1702 0.1978 -0.86 0.38964
## sp5 X1 0.4623 0.3792 1.22 0.22281
## sp6 (Intercept) 0.2006 0.1902 1.05 0.29152
## sp6 X1 1.5796 0.3863 4.09 4.3e-05 ***
## sp7 (Intercept) 0.0180 0.1775 0.10 0.91941
## sp7 X1 -0.3499 0.3488 -1.00 0.31576
## sp8 (Intercept) 0.1588 0.1412 1.12 0.26069
## sp8 X1 0.1323 0.2627 0.50 0.61452
## sp9 (Intercept) 0.0264 0.1703 0.15 0.87699
## sp9 X1 1.1001 0.3269 3.36 0.00077 ***
## sp10 (Intercept) -0.0525 0.1735 -0.30 0.76199
## sp10 X1 -0.5166 0.3234 -1.60 0.11022
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Update model (change main effects to quadratic effects):
model2 <- update(model, env_formula = ~I(X1^2))
summary(model2)
## LogLik: -600.4297
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.2870 1.0000
## sp3 -0.0050 -0.2600 1.0000
## sp4 0.0600 -0.3630 0.5690 1.0000
## sp5 0.4710 -0.3350 -0.0270 -0.0520 1.0000
## sp6 -0.0310 0.4350 0.2190 0.0140 -0.0410 1.0000
## sp7 0.4280 -0.2050 0.1700 0.0730 0.5290 0.2020 1.0000
## sp8 0.2530 0.0580 -0.2890 -0.3710 0.3270 0.0220 0.2400 1.0000
## sp9 0.0550 0.1120 0.0980 0.1210 -0.3220 0.0230 -0.2450 -0.1590 1.0000
## sp10 0.2720 0.2180 -0.4960 -0.3520 0.2270 0.0360 0.1420 0.3030 -0.1140 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7
## X1:X2 0.1946324 -0.462581 0.4739597 -0.1982521 0.4937007 0.1960442 0.4032983
## sp8 sp9 sp10
## X1:X2 0.2994181 0.2302684 -0.006441596
##
##
##
## Estimate Std.Err Z value Pr(>|z|)
## sp1 (Intercept) -0.1307 0.2899 -0.45 0.65
## sp1 I(X1^2) 0.4196 0.7427 0.56 0.57
## sp2 (Intercept) -0.2218 0.3048 -0.73 0.47
## sp2 I(X1^2) 0.6981 0.7684 0.91 0.36
## sp3 (Intercept) -0.3121 0.2963 -1.05 0.29
## sp3 I(X1^2) 0.1102 0.7289 0.15 0.88
## sp4 (Intercept) -0.2547 0.2787 -0.91 0.36
## sp4 I(X1^2) 0.7601 0.6738 1.13 0.26
## sp5 (Intercept) -0.1277 0.2489 -0.51 0.61
## sp5 I(X1^2) 0.2279 0.6497 0.35 0.73
## sp6 (Intercept) 0.1619 0.2606 0.62 0.53
## sp6 I(X1^2) -0.0363 0.6880 -0.05 0.96
## sp7 (Intercept) 0.0430 0.2347 0.18 0.85
## sp7 I(X1^2) -0.0318 0.6161 -0.05 0.96
## sp8 (Intercept) -0.0196 0.2080 -0.09 0.93
## sp8 I(X1^2) 0.7520 0.5211 1.44 0.15
## sp9 (Intercept) 0.2057 0.2406 0.85 0.39
## sp9 I(X1^2) -0.6158 0.5886 -1.05 0.30
## sp10 (Intercept) -0.1004 0.2440 -0.41 0.68
## sp10 I(X1^2) 0.2091 0.5959 0.35 0.73Estimate and visualize meta-community structure:
anv <- anova(model)
plot(anv, internal=TRUE)
## Registered S3 methods overwritten by 'ggtern':
## method from
## grid.draw.ggplot ggplot2
## plot.ggplot ggplot2
## print.ggplot ggplot2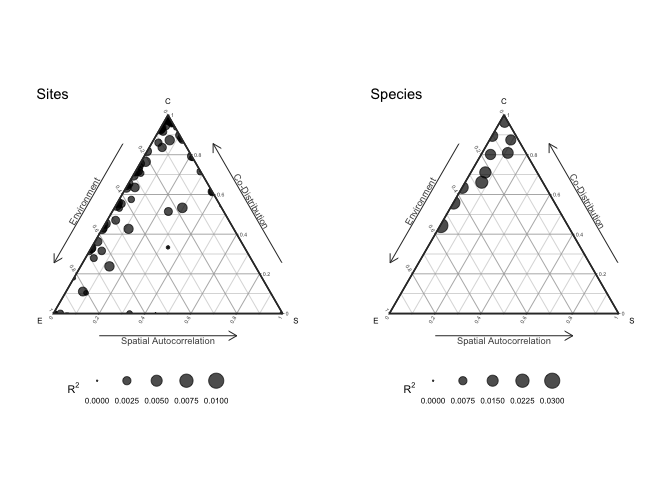
Change linear part of model to a deep neural network:
DNN <- sjSDM(Y = Occ, env = DNN(data = Env, formula = ~.), spatial = linear(data = SP, formula = ~0+X1:X2), se = TRUE, family=binomial("probit"), sampling = 100L)
summary(DNN)
## LogLik: -507.1421
## Regularization loss: 0
##
## Species-species correlation matrix:
##
## sp1 1.0000
## sp2 -0.4000 1.0000
## sp3 -0.1060 -0.3570 1.0000
## sp4 -0.0650 -0.3470 0.7530 1.0000
## sp5 0.5770 -0.3450 -0.1110 -0.0710 1.0000
## sp6 -0.2720 0.3630 0.2170 0.2060 -0.0600 1.0000
## sp7 0.4220 -0.1520 0.1560 0.1970 0.4780 0.2430 1.0000
## sp8 0.2150 0.1140 -0.4060 -0.4120 0.2190 -0.0540 0.0890 1.0000
## sp9 -0.0390 -0.0630 0.0980 0.0970 -0.3440 -0.2930 -0.1830 -0.1220 1.0000
## sp10 0.1270 0.3730 -0.6080 -0.5760 0.2280 0.0620 0.0820 0.3760 -0.2510 1.0000
##
##
##
## Spatial:
## sp1 sp2 sp3 sp4 sp5 sp6 sp7
## X1:X2 0.1791221 -0.5187001 0.5328111 -0.1147005 0.3768144 0.2153512 0.528778
## sp8 sp9 sp10
## X1:X2 0.4690367 0.2996197 0.2277844
##
##
##
## Env architecture:
## ===================================
## Layer_1: (4, 10)
## Layer_2: ReLU
## Layer_3: (10, 10)
## Layer_4: ReLU
## Layer_5: (10, 10)
## Layer_6: ReLU
## Layer_7: (10, 10)
## ===================================
## Weights : 340