The goal of skewlmm is to fit skew robust linear mixed models, using scale mixture of skew-normal linear mixed models with possible within-subject dependence structure, using an EM-type algorithm. In addition, some tools for model adequacy evaluation are available.
For more information about the model formulation and estimation, please see Schumacher, F. L., Lachos, V. H., and Matos, L. A. (2021). Scale mixture of skew‐normal linear mixed models with within‐subject serial dependence. Statistics in Medicine. DOI: 10.1002/sim.8870.
You can install skewlmm from GitHub with:
Or you can install the released version of skewlmm from CRAN with:
This is a basic example which shows you how to fit a SMSN-LMM:
library(skewlmm)
#> Loading required package: optimParallel
#> Loading required package: parallel
dat1 <- as.data.frame(nlme::Orthodont)
fm1 <- smsn.lmm(dat1, formFixed = distance ~ age, formRandom = ~ age,
groupVar = "Subject", distr = "st",
control = lmmControl(quiet = TRUE))
summary(fm1)
#> Linear mixed models with distribution st and dependency structure UNC
#> Call:
#> smsn.lmm(data = dat1, formFixed = distance ~ age, groupVar = "Subject",
#> formRandom = ~age, distr = "st", control = lmmControl(quiet = TRUE))
#>
#> Distribution st with nu = 4.662322
#>
#> Random effects:
#> Formula: ~age
#> Structure:
#> Estimated variance (D):
#> (Intercept) age
#> (Intercept) 6.5378405 -0.55063271
#> age -0.5506327 0.07893263
#>
#> Fixed effects: distance ~ age
#> with approximate confidence intervals
#> Value Std.error CI 95% lower CI 95% upper
#> (Intercept) 17.0163263 0.9456853 15.1628172 18.8698354
#> age 0.6248518 0.1242525 0.3813214 0.8683822
#>
#> Dependency structure: UNC
#> Estimate(s):
#> sigma2
#> 0.81705
#>
#> Skewness parameter estimate: -3.000814 2.202111
#>
#> Model selection criteria:
#> logLik AIC BIC
#> -209.837 437.675 461.814
#>
#> Number of observations: 108
#> Number of groups: 27
plot(fm1)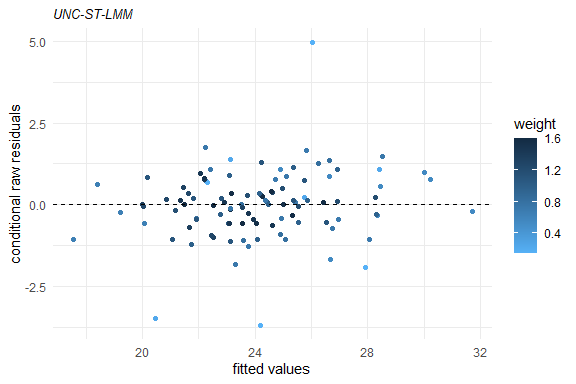
Several methods are available for SMSN and SMN objects, such as: print, summary, plot, fitted, residuals, predict, and update.
Some tools for goodness-of-fit assessment are also available, for example:
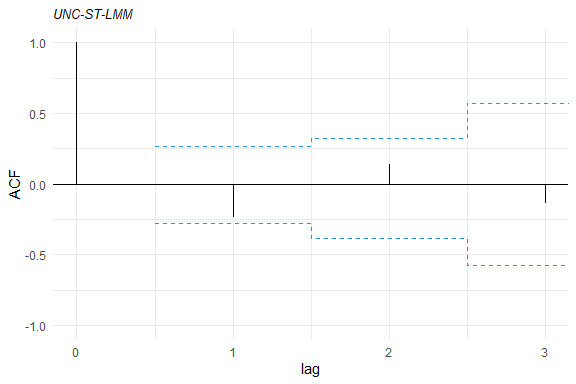
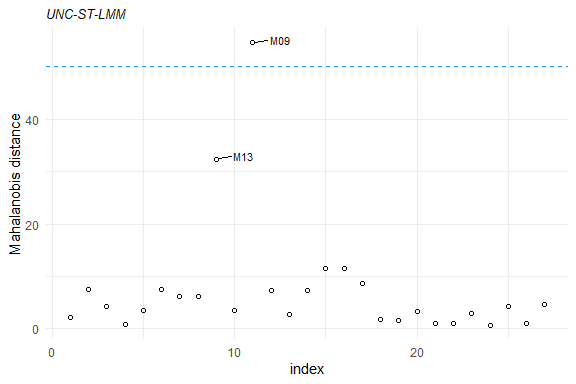
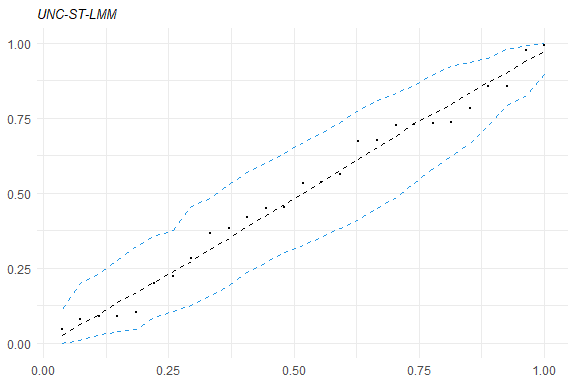
Furthermore, to fit a SMN-LMM one can use the following:
fm2 <- smn.lmm(dat1, formFixed = distance ~ age, formRandom = ~ age,
groupVar = "Subject", distr = "t",
control = lmmControl(quiet = TRUE))
summary(fm2)
#> Linear mixed models with distribution t and dependency structure UNC
#> Call:
#> smn.lmm(data = dat1, formFixed = distance ~ age, groupVar = "Subject",
#> formRandom = ~age, distr = "t", control = lmmControl(quiet = TRUE))
#>
#> Distribution t with nu = 4.966122
#>
#> Random effects:
#> Formula: ~age
#> Structure:
#> Estimated variance (D):
#> (Intercept) age
#> (Intercept) 3.2735098 -0.16423589
#> age -0.1642359 0.03246643
#>
#> Fixed effects: distance ~ age
#> with approximate confidence intervals
#> Value Std.error CI 95% lower CI 95% upper
#> (Intercept) 17.274030 0.67741340 15.9463240 18.6017357
#> age 0.593514 0.06218718 0.4716294 0.7153986
#>
#> Dependency structure: UNC
#> Estimate(s):
#> sigma2
#> 0.8926729
#>
#> Model selection criteria:
#> logLik AIC BIC
#> -211.351 436.701 455.476
#>
#> Number of observations: 108
#> Number of groups: 27Now, for performing a LRT for testing if the skewness parameter is 0 (H0 : λi = 0, ∀i), one can use the following:
lr.test(fm1,fm2)
#>
#> Model selection criteria:
#> logLik AIC BIC
#> fm1 -209.837 437.675 461.814
#> fm2 -211.351 436.701 455.476
#>
#> Likelihood-ratio Test
#>
#> chi-square statistics = 3.026434
#> df = 2
#> p-value = 0.2202005
#>
#> The null hypothesis that both models represent the
#> data equally well is not rejected at level 0.05By default, the functions smsn.lmm and smn.lmm now use the DAAREM method (a method for EM accelaration, for details see help(package="daarem")) for estimation, to improve the computational performance. This method usually greatly reduces the convergence time, but its use can result in numerical errors, specially for small samples. In this cases, the EM algorithm can be used, as follows:
fm2EM <- smn.lmm(dat1, formFixed = distance ~ age, formRandom = ~ age, distr = 't',
groupVar = "Subject", control = lmmControl(algorithm = "EM",
quiet = TRUE))
fm2EM
#> Linear mixed models with distribution t and dependency structure UNC
#> Call:
#> smn.lmm(data = dat1, formFixed = distance ~ age, groupVar = "Subject",
#> formRandom = ~age, distr = "t", control = lmmControl(algorithm = "EM",
#> quiet = TRUE))
#>
#> Fixed: distance ~ age
#> Random:
#> Formula: ~age
#> Structure: General positive-definite
#> Estimated variance (D):
#> (Intercept) age
#> (Intercept) 3.1584628 -0.1533659
#> age -0.1533659 0.0314773
#>
#> Estimated parameters:
#> (Intercept) age sigma2 Dsqrt11 Dsqrt12 Dsqrt22 nu1
#> 17.2876 0.5958 0.8982 1.7754 -0.0793 0.1587 4.9883
#> s.e. 0.6684 0.0616 0.2460 0.8421 0.0931 0.0518 NA
#>
#> Model selection criteria:
#> logLik AIC BIC
#> -211.351 436.701 455.476
#>
#> Number of observations: 108
#> Number of groups: 27Also, we can fit a t-LMM with diagonal scale matrix for the random effects by using:
fm2diag <- update(fm2, covRandom = "pdDiag")
fm2diag
#> Linear mixed models with distribution t and dependency structure UNC
#> Call:
#> smn.lmm(data = dat1, formFixed = distance ~ age, groupVar = "Subject",
#> formRandom = ~age, distr = "t", covRandom = "pdDiag", control = lmmControl(quiet = TRUE))
#>
#> Fixed: distance ~ age
#> Random:
#> Formula: ~age
#> Structure: Diagonal
#> Estimated variance (D):
#> (Intercept) age
#> (Intercept) 1.546268 0.00000000
#> age 0.000000 0.01789115
#>
#> Estimated parameters:
#> (Intercept) age sigma2 Dsqrt11 Dsqrt22 nu1
#> 17.2827 0.5959 0.9699 1.2435 0.1338 4.9841
#> s.e. 0.5864 0.0540 0.2388 0.6191 0.0551 NA
#>
#> Model selection criteria:
#> logLik AIC BIC
#> -211.598 435.197 451.29
#>
#> Number of observations: 108
#> Number of groups: 27We can compare the information criteria for all fitted models using the criteria function, as follows:
criteria(list(`ST-LMM` = fm1, `t-LMM` = fm2, `t-LMM(EM)` = fm2EM, `t-LMM-diag` = fm2diag))
#> logLik npar AIC BIC
#> ST-LMM -209.8374 9 437.6748 461.8140
#> t-LMM -211.3506 7 436.7012 455.4761
#> t-LMM(EM) -211.3506 7 436.7013 455.4762
#> t-LMM-diag -211.5985 6 435.1969 451.2897For more examples, see help(smsn.lmm) and help(smn.lmm).